Objective value for the variance criterion

Compute the k-means variance objective for a given clustering.

variance_objective(x, clusters)

Arguments

x

A vector, matrix or data.frame of data points. Rows correspond to elements and columns correspond to features. A vector represents a single feature.

clusters

A vector representing (anti)clusters (e.g., returned by anticlustering or balanced_clustering)

Value

The total within-cluster variance

Details

The variance objective is given by the sum of the squared errors between cluster centers and individual data points. It is the objective function used in k-means clustering, see kmeans.

References

Jain, A. K. (2010). Data clustering: 50 years beyond k-means. Pattern Recognition Letters, 31, 651–666.

Papenberg, M., & Klau, G. W. (2021). Using anticlustering to partition data sets into equivalent parts. Psychological Methods, 26(2), 161–174. https://doi.org/10.1037/met0000301.

Späth, H. (1986). Anticlustering: Maximizing the variance criterion. Control and Cybernetics, 15, 213–218.

Author

Martin Papenberg martin.papenberg@hhu.de

Examples

data(iris)
## Clustering
clusters <- balanced_clustering(
  iris[, -5],
  K = 3
)
# This is low:
variance_objective(
  iris[, -5],
  clusters
)
#> [1] 81.6306
## Anticlustering
anticlusters <- anticlustering(
  iris[, -5],
  K = 3,
  objective = "variance"
)
# This is higher:
variance_objective(
  iris[, -5],
  anticlusters
)
#> [1] 681.3698

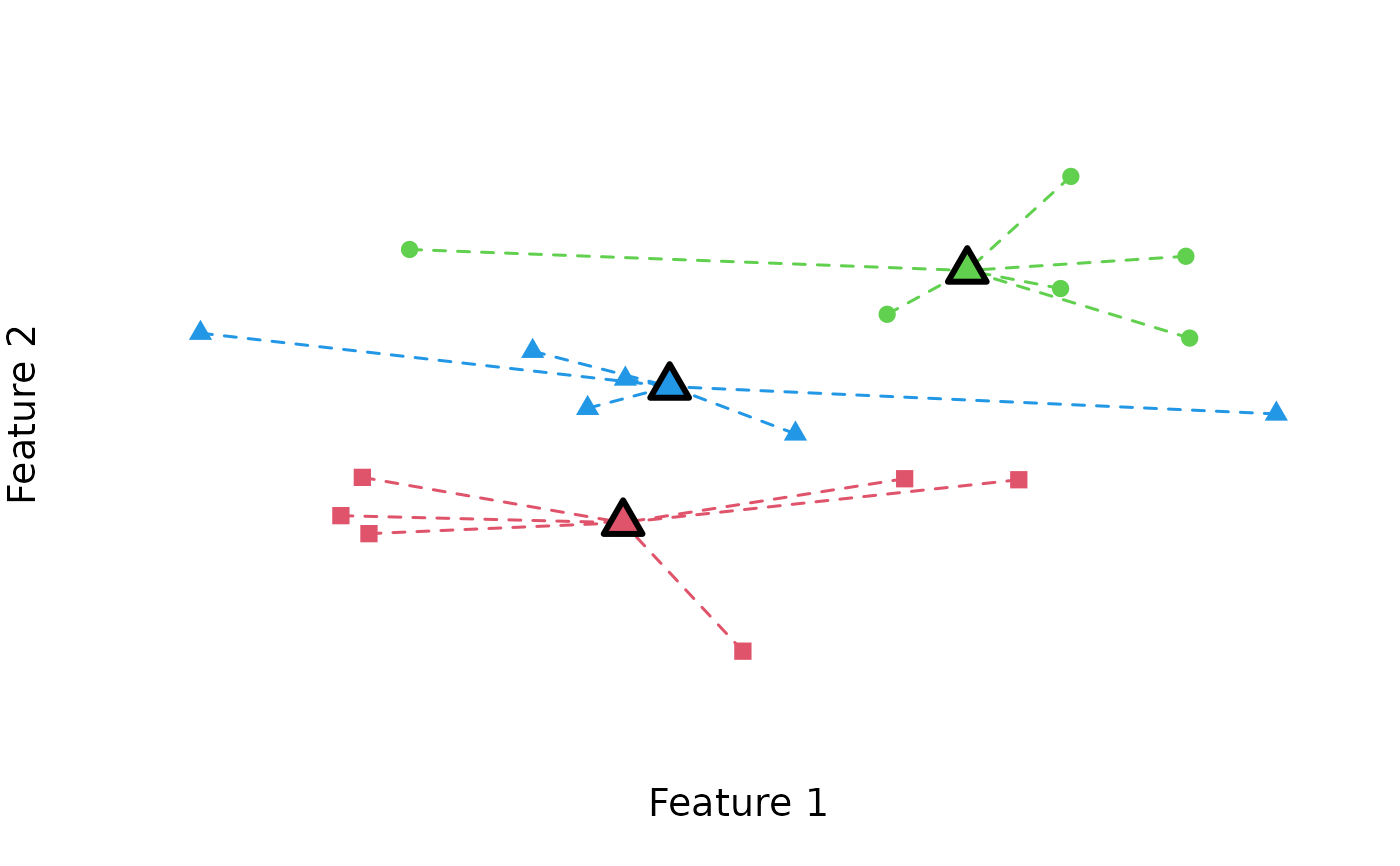
# Illustrate variance objective
N <- 18
data <- matrix(rnorm(N * 2), ncol = 2)
cl <- balanced_clustering(data, K = 3)
plot_clusters(data, cl, illustrate_variance = TRUE)