Using the R package anticlust for stimulus selection in experiments

This tutorial teaches you how to use the R package anticlust for stimulus selection in psychological experiments. All code can easily be reproduced via Copy & Paste. The tutorial discusses the following functionalities:

Match similar stimuli based on covariates of interest
Minimize differences between stimulus sets with regard to some variables
Maximize differences between stimulus sets with regard to some variables
Balance the occurrence of a categorical variable between stimulus sets

To follow the code in this tutorial, load the anticlust package first:

library(anticlust)

For the examples in this document, we use norming data for a stimulus set provided by Schaper, Kuhlmann and Bayen (2019a, 2019b). It is available when the package anticlust is loaded:

data("schaper2019")
# look at the data
head(schaper2019)
#>                 item     room rating_consistent rating_inconsistent syllables
#> 1 Feuchtigkeitsmaske bathroom              4.10                1.04         5
#> 2        Damenbinden bathroom              4.22                1.12         4
#> 3          Haarspray bathroom              4.32                1.13         2
#> 4             Tampon bathroom              4.35                1.22         2
#> 5          Badewanne bathroom              4.55                1.02         4
#> 6     Ohrenstaebchen bathroom              4.63                1.26         4
#>   frequency list
#> 1        21    1
#> 2        19    1
#> 3        17    1
#> 4        17    1
#> 5        13    1
#> 6        21    1

The item pool consists of 96 German words, given in the column item. Each word represents an object that is either typically found in a bathroom or in a kitchen. For their experiments, Schaper et al. partitioned the pool into 3 word lists that should be as similar as possible with regard to four numeric criteria (that is: rating_consistent, rating_inconsistent, syllables, frequency). Typically, stimulus sets may contain more than 96 elements (and the selection usually becomes more effective when the pool is larger), but the logic for stimulus selection that is applied in this tutorial can be transfered to arbitrarily large stimulus sets.

Example 1a: Maximize differences in frequency

In the first example, I select two word lists that differ on frequency but are as similar as possible with regard to consistency ratings and the number of syllables. First, I need to define the boundaries that define “high” and “low” frequency. Note that frequency is reverse-coded such that low values actually indicate high frequency. Here, I arbitrarily define values below 18 as “high” frequency and above 19 as “low” frequency, but any user-defined splits are possible.

schaper2019 <- within(schaper2019, {
  freq <- ifelse(frequency < 18, "high", NA)
  freq <- ifelse(frequency > 19, "low", freq)
})

This code defined a new column freq for the data set schaper2019 that is either “low”, “high” or missing (NA). Let’s check it out:

schaper2019$freq
#>  [1] "low"  NA     "high" "high" "high" "low"  NA     "high" "high" "low" 
#> [11] NA     "low"  "high" "high" NA     "high" "high" "high" "low"  "low" 
#> [21] "high" "low"  "high" "high" "low"  NA     "low"  "high" "low"  "high"
#> [31] NA     "high" "high" "high" NA     NA     "low"  NA     "low"  "high"
#> [41] "low"  NA     "low"  "high" "low"  "high" NA     NA     NA     NA    
#> [51] NA     "low"  "low"  "low"  NA     "high" "high" "low"  "low"  "low" 
#> [61] "low"  NA     "high" "high" NA     "low"  NA     "low"  NA     NA    
#> [71] "low"  NA     NA     "low"  "low"  NA     NA     "high" "high" NA    
#> [81] "low"  "low"  NA     "low"  "high" "high" NA     "high" "low"  "high"
#> [91] NA     NA     "high" NA     NA     "high"

Before matching high and low frequency words, it is necessary to remove cases that are not selected, i.e. where the entry in freq is NA:

selected <- subset(schaper2019, !is.na(freq))
# see how many cases were selected:
table(selected$freq)
#> 
#> high  low 
#>   33   31

Now, I use the anticlust function matching() to find paired words of high and low frequency that are as similar as possible on consistency and the number of syllables:

# Match the conditions based on covariates
covariates <- scale(selected[, 3:5])
selected$matches <- matching(
  covariates, 
  match_between = selected$freq,
  match_within = selected$room,
  match_extreme_first = FALSE
)

The first argument defines the covariates that should be similar in both sets. I used the function scale() before passing the covariates to the matching function to standardize the variables. This way, each variable has the same weight in the matching process, which is usually desirable. The argument match_between is the grouping variable based on frequency that I just defined. The argument match_within is used to ensure that matches are selected between words belonging to the same room. The argument match_extreme_first is used to guide the behaviour of the matching algorithm, but its precise meaning is not important for now (for more information, see ?matching). Generally, if we plan to only keep a subset of all matches – as we do in the current application –, we set match_extreme_first to FALSE. If we want to keep all elements, match_extreme_first = TRUE is usually better.

Next, let us check out some of the matches we created:

subset(selected, matches == 1)
#>            item     room rating_consistent rating_inconsistent syllables
#> 12     Wattepad bathroom              4.39                1.14         3
#> 44 Rasierschaum bathroom              4.39                1.16         3
#>    frequency list freq matches
#> 12        21    1  low       1
#> 44        17    2 high       1
subset(selected, matches == 2)
#>             item    room rating_consistent rating_inconsistent syllables
#> 29 Zuckerstreuer kitchen              4.48                1.04         4
#> 86    Mikrowelle kitchen              4.58                1.04         4
#>    frequency list freq matches
#> 29        21    1  low       2
#> 86        15    3 high       2

The matches are numbered by similarity, meaning that matches with grouping number 1 are most similar. Therefore, we can easily select the 8 best-matched groups of words that we would like include in our experiment:

# Select the 8 best matches:
final_selection <- subset(selected, matches <= 8)

Last, we check the quality of the results by investigating the descriptive statistics – means and standard deviations (in brackets) – by condition:

# Check quality of the selection:
mean_sd_tab(
  final_selection[, 3:6], 
  final_selection$freq
)

	rating_consistent	rating_inconsistent	syllables	frequency
high	4.39 (0.17)	1.10 (0.05)	3.50 (0.53)	16.25 (0.71)
low	4.38 (0.14)	1.09 (0.03)	3.50 (0.53)	21.12 (0.64)

The descriptive statistics are similar across the sets for the consistency ratings and the number of syllables, and dissimilar for frequency, which is good. In general, the results can even be improved if we can select from a larger item pool (then, more matches are possible).

If we are not sure how many items should be part of our experiment, the function plot_similarity() may help. It plots an index of similarity (see ?plot_similarity) for each match:

plot_similarity(
  covariates, 
  groups = selected$matches
)

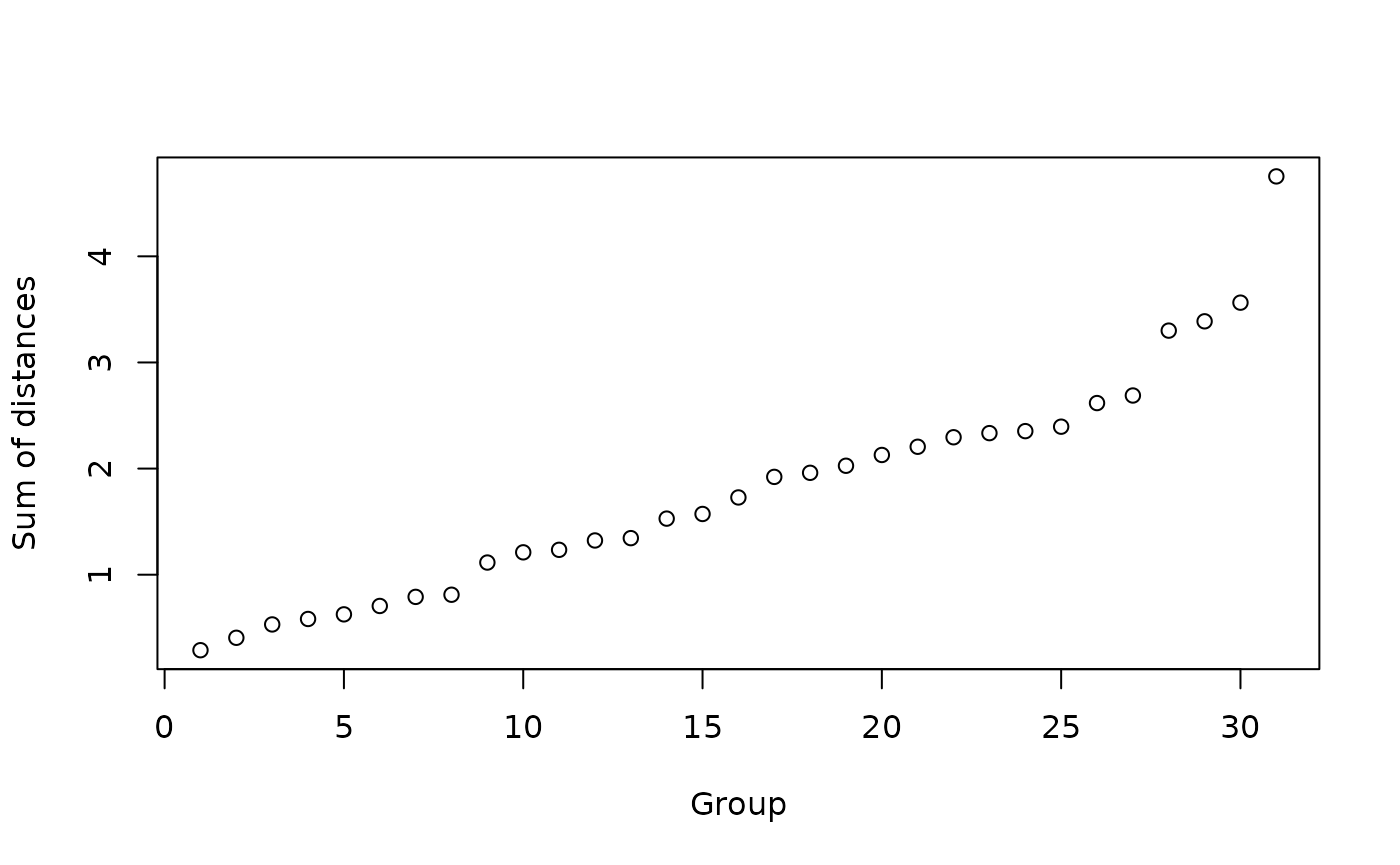
The figure depicts the sum of pairwise dissimilarities (based on the Euclidean distance) variance per match; the larger the value, the less homogenous the match. It seems indeed that the first eight matches are most similar; after the 8th match, there is already a notable decline in similarity.

Example 1b: Two-factorial design

# Reload the data for next example
data("schaper2019")

In another example, we construct a two-factorial design: we create groups that differ on rating_consistent and rating_inconsistent (these properties are orthogonally crossed) but are similar on frequency and the number of syllables. First, we categorize the variables frequency and syllables into two levels, respectively. This time, I just use median splits, which means that I do not exclude any data in this first step:

schaper2019 <- within(schaper2019, {
  incon <- ifelse(rating_inconsistent < median(rating_inconsistent), "low incon", NA)
  incon <- ifelse(rating_inconsistent >= median(rating_inconsistent), "high incon", incon)
  con <- ifelse(rating_consistent <= median(rating_consistent), "low con", NA)
  con <- ifelse(rating_consistent > median(rating_consistent), "high con", con)
})

Let us check how many words are left per condition:

table(schaper2019$con, schaper2019$incon)
#>           
#>            high incon low incon
#>   high con         26        22
#>   low con          27        21

Next, we conduct a matching between the four groups that resulted from crossing frequency and syllables:

# Match the conditions based on covariates
covariates <- scale(schaper2019[, c("frequency", "syllables")])
schaper2019$matches <- matching(
  covariates, 
  match_between = schaper2019[, c("con", "incon")],
  match_extreme_first = FALSE
)

In this application, each match consists of 4 words because we have 4 conditions, e.g.:

subset(schaper2019, matches == 1)
#>            item     room rating_consistent rating_inconsistent syllables
#> 7    Klobuerste bathroom              4.82                1.04         3
#> 47 Kloschuessel bathroom              4.84                1.13         3
#> 51 Sparschaeler  kitchen              4.32                1.00         3
#> 57   Kastenform  kitchen              4.10                1.18         3
#>    frequency list      con      incon matches
#> 7         18    1 high con  low incon       1
#> 47        18    2 high con high incon       1
#> 51        18    2  low con  low incon       1
#> 57        17    2  low con high incon       1

To decide how many matched groups we would like to keep, let’s check out the similarity plot:

# Plot covariate similarity by match:
plot_similarity(covariates, schaper2019$matches)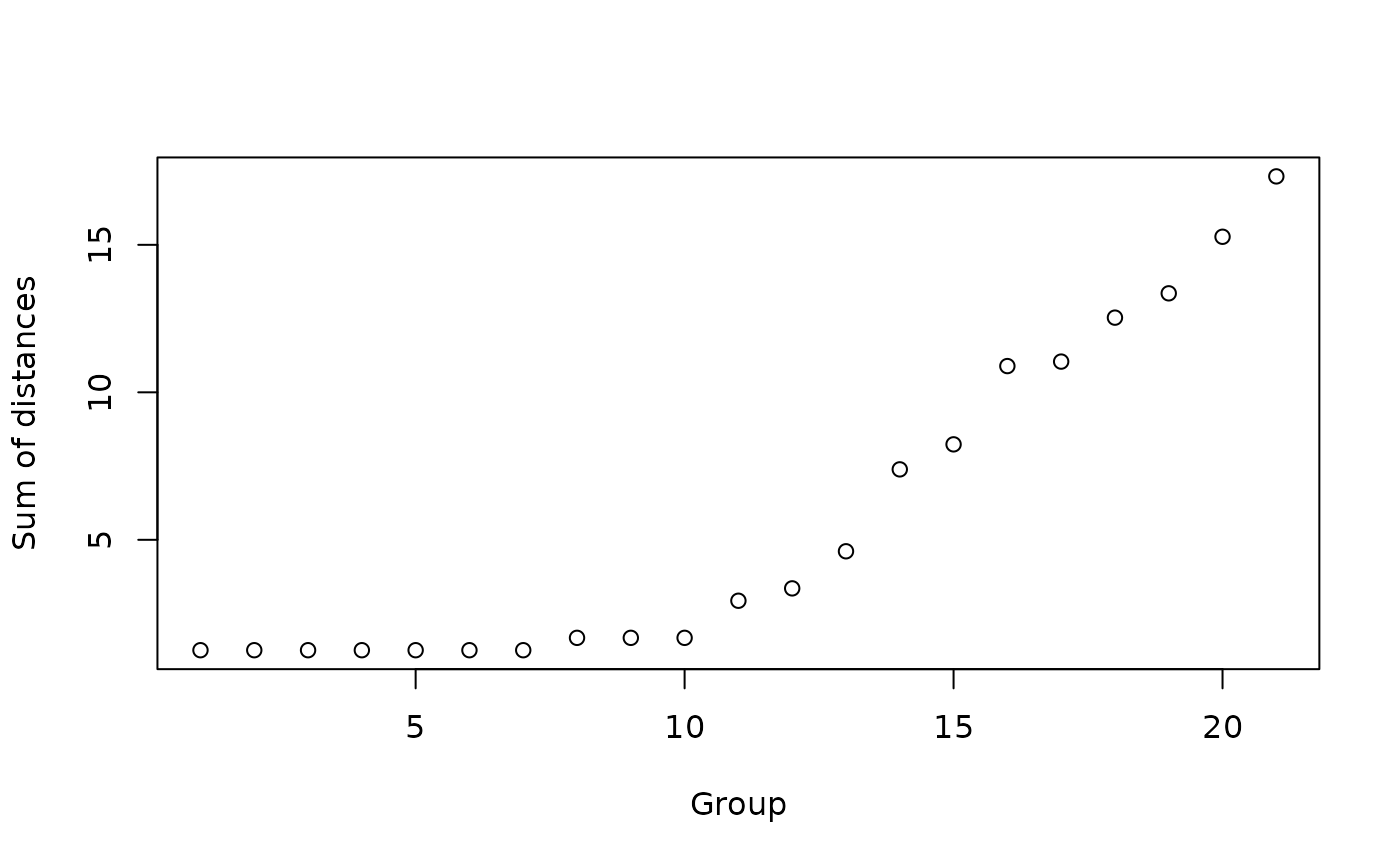

Based on the plot, we select the 10 best matches:

# Select the 5 best matches:
final_selection <- subset(schaper2019, matches <= 10)

Last, we check quality of the selection by printing the descriptive statistics by condition:

mean_sd_tab(
  subset(final_selection, select = 3:6), 
  paste(final_selection$con, final_selection$incon)
)

	rating_consistent	rating_inconsistent	syllables	frequency
high con high incon	4.68 (0.15)	1.15 (0.06)	3.40 (0.70)	19.10 (1.85)
high con low incon	4.70 (0.18)	1.04 (0.03)	3.40 (0.70)	18.90 (1.45)
low con high incon	4.32 (0.09)	1.17 (0.04)	3.40 (0.70)	18.90 (1.66)
low con low incon	4.26 (0.11)	1.04 (0.03)	3.40 (0.70)	18.80 (1.55)

Again, the covariates are quite similar between sets, but with a larger item pool even better results could be achieved.

Example 2: Anticlustering

# Reload the data for next example
data("schaper2019")

In the next example, we wish to partition the entire pool of 96 items into 3 sets that are as similar as possible on all variables. That means that there is no independent variable that varies between conditions; the experimental manipulation is independent of the intrinsic stimulus properties. Creating stimulus sets that are overall similar to each other can be done using anticlustering (Papenberg & Klau, 2020):

## Conduct anticlustering (assign all items to three similar groups)
schaper2019$anticluster <- anticlustering(
  schaper2019[, 3:6], 
  K = 3,
  objective = "variance"
)

## check out quality of the solution
mean_sd_tab(
  subset(schaper2019, select = 3:6), 
  schaper2019$anticluster
)

	rating_consistent	rating_inconsistent	syllables	frequency
1	4.49 (0.27)	1.10 (0.07)	3.41 (0.84)	18.31 (2.90)
2	4.49 (0.23)	1.10 (0.07)	3.44 (0.88)	18.31 (2.25)
3	4.49 (0.25)	1.10 (0.06)	3.41 (1.07)	18.31 (1.99)

Example 2b: Anticlustering on subset selection

# Reload the data for next example
data("schaper2019")

If we do not want to include all 96 words in our experiment, we can again use the matching() function to select a subset of similar stimuli that we employ. Again, we wish the select three groups that are as similar as possible on all variables, but we only use a subset of all 96 items. To achieve this goal, we create triplets of similar stimuli using matching(); afterwards, the items belonging to the same triplet will be assigned to different experimental sets. We use the argument match_within to ensure that all triplets consist of items belonging to the same room:

# First, identify triplets of similar word, within room
covariates <- scale(schaper2019[, 3:6])
schaper2019$triplet <- matching(
  covariates,
  p = 3,
  match_within = schaper2019$room
)

# check out the two most similar triplets:
subset(schaper2019, triplet == 1)
#>             item    room rating_consistent rating_inconsistent syllables
#> 19  Kaffeebeutel kitchen              4.31                1.04         4
#> 58   Kaesemesser kitchen              4.28                1.04         4
#> 59 Cerankochfeld kitchen              4.34                1.04         4
#>    frequency list triplet
#> 19        22    1       1
#> 58        21    2       1
#> 59        21    2       1
subset(schaper2019, triplet == 2)
#>             item    room rating_consistent rating_inconsistent syllables
#> 27  Buttermesser kitchen              4.40                1.00         4
#> 29 Zuckerstreuer kitchen              4.48                1.04         4
#> 53  Salatbesteck kitchen              4.48                1.02         4
#>    frequency list triplet
#> 27        21    1       2
#> 29        21    1       2
#> 53        20    2       2

# Select the 10 best triplets
best <- subset(schaper2019, triplet <= 10)

Now, we use anticlustering() to assign the matched words to different sets:

best$anticluster <- anticlustering(
  best[, 3:6], 
  K = 3,
  categories = best$triplet,
  objective = "variance"
)

In this function call, we pass the triplets to the argument categories, thus ensuring that the matched items are assigned to different sets. We can confirm this worked by looking at the cross table of triplet and anticluster:

table(best$triplet, best$anticluster)
#>     
#>      1 2 3
#>   1  1 1 1
#>   2  1 1 1
#>   3  1 1 1
#>   4  1 1 1
#>   5  1 1 1
#>   6  1 1 1
#>   7  1 1 1
#>   8  1 1 1
#>   9  1 1 1
#>   10 1 1 1

Anticlustering strives to assign the matched triplets to the different sets in such a way that all sets are as similar as possible. Note that by ensuring that the triplets only consisted of items from the same room, the room was also balanced across anticlusters:

table(best$room, best$anticluster)
#>           
#>            1 2 3
#>   bathroom 5 5 5
#>   kitchen  5 5 5

Last, we check out the descriptive statistics by anticluster, confirming that the sets are indeed quite similar on all numeric attributes:

## check out quality of the solution
mean_sd_tab(
  subset(best, select = 3:6), 
  best$anticluster
)

	rating_consistent	rating_inconsistent	syllables	frequency
1	4.46 (0.27)	1.08 (0.05)	3.50 (0.97)	19.00 (3.02)
2	4.47 (0.28)	1.08 (0.05)	3.50 (1.18)	19.00 (2.67)
3	4.46 (0.22)	1.08 (0.06)	3.50 (0.97)	18.90 (2.28)

References

Papenberg, M., & Klau, G. W. (2021). Using anticlustering to partition data sets into equivalent parts. Psychological Methods, 26(2), 161–174. https://doi.org/10.1037/met0000301

Schaper, M. L., Kuhlmann, B. G., & Bayen, U. J. (2019a). Metacognitive expectancy effects in source monitoring: Beliefs, in-the-moment experiences, or both? Journal of Memory and Language, 107, 95–110. https://doi.org/10.1016/j.jml.2019.03.009

Schaper, M. L., Kuhlmann, B. G., & Bayen, U. J. (2019b). Metamemory expectancy illusion and schema-consistent guessing in source monitoring. Journal of Experimental Psychology: Learning, Memory, and Cognition, 45, 470. https://doi.org/10.1037/xlm0000602

Martin Papenberg

Example 1a: Maximize differences in frequency

Example 1b: Two-factorial design

Example 2: Anticlustering

Example 2b: Anticlustering on subset selection

References