Create balanced clusters of equal size

balanced_clustering(x, K, method = "centroid", solver = NULL)

Source

The centroid method was originally developed and contributed by Meik Michalke. It was later rewritten by Martin Papenberg, who also implemented the integer linear programming method.

Arguments

x: The data input. Can be one of two structures: (1) A feature matrix where rows correspond to elements and columns correspond to variables (a single numeric variable can be passed as a vector). (2) An N x N matrix dissimilarity matrix; can be an object of class dist (e.g., returned by dist or as.dist) or a matrix where the entries of the upper and lower triangular matrix represent pairwise dissimilarities.
K: How many clusters should be created.
method: One of "centroid" or "ilp". See Details.
solver: Optional. The solver used to obtain the optimal method if method = "ilp". Currently supports "glpk" and "symphony". Is ignored for method = "centroid".

Value

An integer vector representing the cluster affiliation of each data point

Details

This function partitions a set of elements into K equal-sized clusters. The function offers two methods: a heuristic and an exact method. The heuristic (method = "centroid") first computes the centroid of all data points. If the input is a feature matrix, the centroid is defined as the mean vector of all columns. If the input is a dissimilarity matrix, the most central element acts as the centroid; the most central element is defined as the element having the minimum maximal distance to all other elements. After identifying the centroid, the algorithm proceeds as follows: The element having the highest distance from the centroid is clustered with its (N/K) - 1 nearest neighbours (neighbourhood is defined according to the Euclidean distance if the data input is a feature matrix). From the remaining elements, again the element farthest to the centroid is selected and clustered with its (N/K) - 1 neighbours; the procedure is repeated until all elements are part of a cluster.

An exact method (method = "ilp") can be used to solve equal-sized weighted cluster editing optimally (implements the integer linear program described in Papenberg and Klau, 2020; (8) - (10), (12) - (13)). The cluster editing objective is the sum of pairwise distances within clusters; clustering is accomplished by minimizing this objective. If the argument x is a features matrix, the Euclidean distance is computed as the basic unit of the cluster editing objective. If another distance measure is preferred, users may pass a self-computed dissimiliarity matrix via the argument x.

The optimal method = "ilp" uses a "solver" to optimize the clustering objective. See optimal_anticlustering for an overview of the solvers that are available.

References

Grötschel, M., & Wakabayashi, Y. (1989). A cutting plane algorithm for a clustering problem. Mathematical Programming, 45, 59–96.

Papenberg, M., & Klau, G. W. (2021). Using anticlustering to partition data sets into equivalent parts. Psychological Methods, 26(2), 161–174. https://doi.org/10.1037/met0000301.

Author

Martin Papenberg martin.papenberg@hhu.de

Meik Michalke meik.michalke@hhu.de

Examples


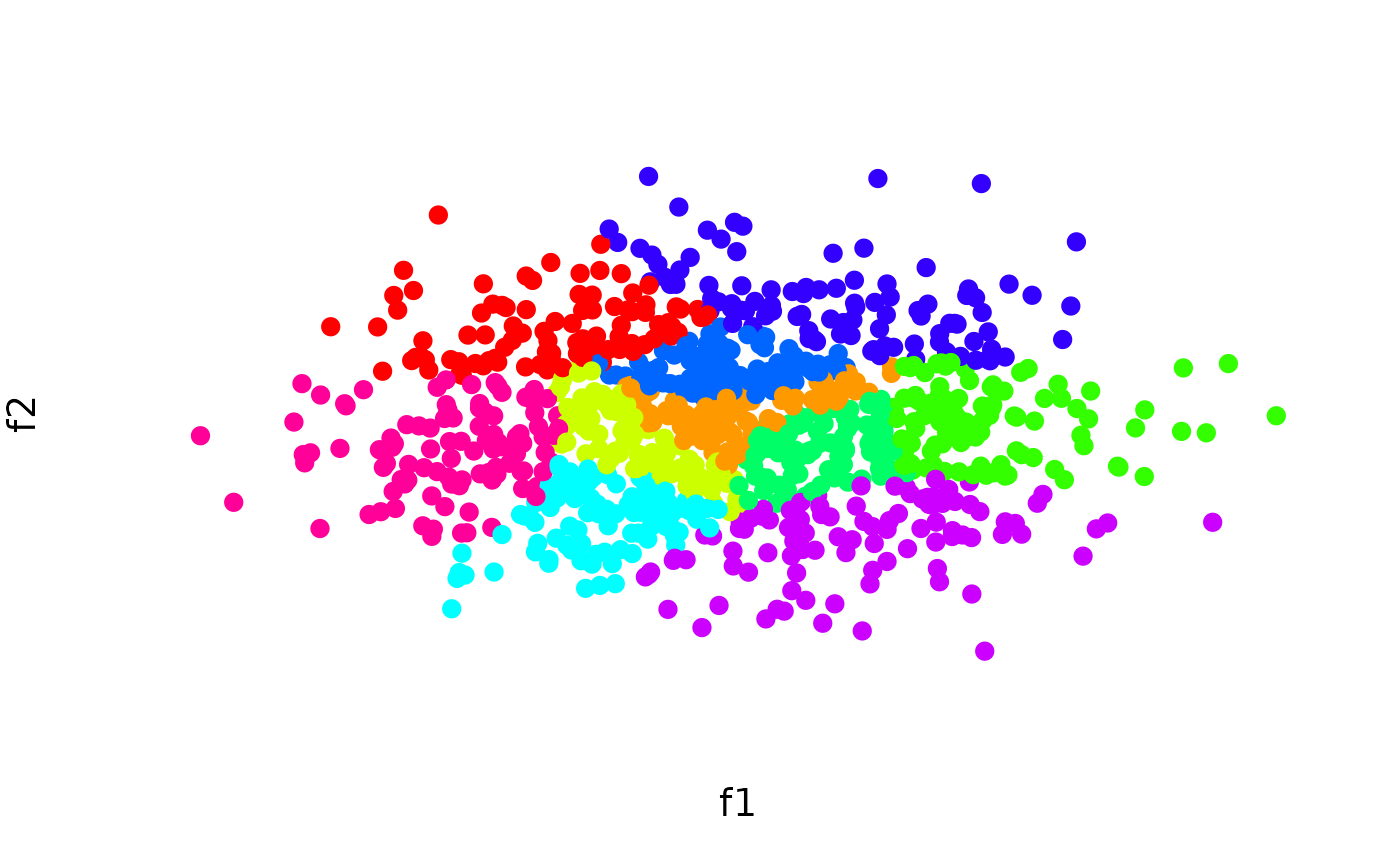
# Cluster a data set and visualize results
N <- 1000
lds <- data.frame(f1 = rnorm(N), f2 = rnorm(N))
cl <- balanced_clustering(lds, K = 10)
plot_clusters(lds, clusters = cl)


# Repeat using a distance matrix as input
cl2 <- balanced_clustering(dist(lds), K = 10)
plot_clusters(lds, clusters = cl2)