2 Vektoren

Die einfachste und wichtigste Datenstruktur von R ist der Vektor. Ein Vektor ist beispielsweise eine einzelne Zahl wie in den Taschenrechner-Berechnungen in Kapitel 1. So gilt für die Berechnung 1 + 3:

  • 1 ist ein Vektor
  • 3 ein Vektor
  • das Ergebnis 4 ist auch ein Vektor

Das Interessante an Vektoren ist, dass der ein-elementige Vektor nur ein Spezialfall ist. Im Normalfall können Vektoren mehrere Elemente enthalten; die „atomare“ Einheit in R ist also nicht ein einzelnes Element, sondern gleich eine Aneinanderreihung beliebig vieler4 gleichartiger Elemente, etwa Zahlen. Statistische Berechnungen – wie die Berechnung eines Mittelwerts oder einer Standardabweichung – lassen sich direkt auf einer Menge an Daten durchführen, da diese in einem Vektor gespeichert sind. Diese „Vektorbasiertheit“ ist vermutlich die größte Stärke von R für statistische Berechnungen.

Elemente zu Vektoren zusammenfügen (sprich: mehrere Vektoren zu einem Vektor zusammenfügen) funktioniert mit der Funktion c() – die vermutlich basalste Funktion in R. Sie ist so simpel und grundlegend, dass man sie gegebenenfalls vergisst, wenn man sie braucht – versucht, sie zu erinnern!

[1] 0.5 1.0 1.5

Man kann die Funktion c() auch auf eine einzelne Zahl anwenden. Das ist dasselbe als würde man nur die Zahl eingeben:

[1] 1

Folgendes geht auch, da c() mehrere Vektoren zu einem einzelnen Vektor „verschmilzt“:

[1] 0.5 1.0 1.5 1.0 2.0 3.0

Auf mehrelementigen Vektoren kann man statistische Berechnungen durchführen, wie etwa die Bestimmung des arithmetischen Mittels, einer Standardabweichung, der Varianz, oder des Minimums oder Maximums:5

[1] 1
[1] 0.5
[1] 0.25
[1] 0.5
[1] 0.5
[1] 1.5

In diesem Code-Block haben wir implizit einen wichtigen Bestandteil von R kennengelernt: Funktionen. Für den Einstieg reicht es für uns, folgende Eigenschaften von Funktionen zu verstehen:

  • Funktionen haben einen Namen – etwa: mean oder c
  • Hinter dem Namen einer Funktion werden in Klammern ein oder mehrere Argumente übergeben, etwa: ein Vektor
  • Wenn einer Funktion mehrere Argumente übergeben werden, werden diese mit Kommata separiert, etwa: c(1, 2, 3)
  • Funktionen führen mit den übergebenen Daten eine Berechnung durch und geben uns das Ergebnis zurück

Einfach gesagt nehmen also Funktionen Daten entgegen und geben wiederum Daten zurück. Der Großteil unserer Arbeit mit R ist die Anwendung von Funktionen. Es ist möglich, Funktionsaufrufe zu verschachteln, wie dieses Beispiel zeigte:

Hier wertet die Funktion sqrt() (die Wurzel; engl. square root) das Ergebnis der Funktion var() aus, um eine Standardabweichnung zu bestimmen. Der Aufruf ist also äquivalent zu sqrt(0.25), da die Varianz von 0.5, 1, und 1.5 gleich 0.25 ist. Diese Beobachtung offenbart eine weitere wichtige Eigenschaft von R: Wir können unseren Code immer als das verstehen, was er ergibt, wenn er von R ausgewertet wird. Es macht keinen Unterschied, ob ich das Ergebnis einer Berechnung selber „händisch“ aufschreibe – also hier 0.25 –, oder Code schreibe, der mir dieses Ergebnis generiert – hier: var(c(0.5, 1, 1.5)).

Eine nützliche und oft verwendete Kurzform, um Vektoren aufsteigender, ganzer Zahlen zu erstellen ist folgende:

 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20

So lässt sich beispielsweise sehr einfach die Summe aller Zahlen von 1 bis 1,000 berechnen:

[1] 500500

Wir können auch absteigende Sequenzen erstellen:

 [1]  5  4  3  2  1  0 -1 -2 -3 -4 -5

Diese Tabelle enthält einige nützliche Funktionen, die auf Vektoren anwendbar sind (in R-Jargon: sie nehmen einen Vektor als Argument an) und jeweils selber auch einen Vektor zurückgeben:

Name Funktionalität
mean Berechnet den Mittelwert eines Vektors
median Berechnet den Median eines Vektors
sum Berechnet die Summe aller Elemente eines Vektors
max Gibt den größten Wert eines Vektors zurück
min Gibt den kleinsten Wert eines Vektors zurück
length Gibt die Zahl der Elemente eines Vektors zurück
sd Berechnet die Standardabweichung eines Vektors
var Berechnet die Varianz eines Vektors
sort Sortiert einen Vektor aufsteigend
rev Kehrt die Reihenfolge der Elemente im Vektor um
round Rundet die Elemente in einem Vektor
sqrt Berechnet für jedes Element im Vektor die Quadratwurzel
unique Gibt alle unterschiedlichen Werte eines Vektors aus

 

Für die Funktionen in dieser Tabelle gilt, dass sie zwar alle einen Vektor zurückgeben, aber die Länge des Ausgabevektors unterschiedlich sein kann. Die Funktionen mean() und sum() ergeben etwa Vektoren der Länge 1, da sie genau einen Kennwert bestimmen. Die Funktionen sort(), sqrt() und round() geben hingegen einen Vektor zurück, der aus genauso vielen Elementen besteht wie der Eingabevektor.

2.1 Vektorisierung

Basale mathematische Berechnungen werden gleich auf alle Elemente eines Vektors angewendet:

 [1]  2  4  6  8 10 12 14 16 18 20
 [1]  1  3  5  7  9 11 13 15 17 19

Hierbei werden die Operationen * 2 bzw. -1 direkt auf alle Elemente der Vektoren 1:10 bzw. (1:10 * 2) angewendet; die Ausgabe ist jeweils ein Vektor der Länge 10. Bei gleich langen Vektoren werden solche Operationen im Allgemeinen komponentenweise angewendet:

[1]  8 15 24

Dieses Verhalten ist typisch für R: Viele Funktionen und Operationen in R arbeiten komponentenweise, wenn zwei Vektoren gleicher Länge übergeben werden. Das Element an Position 1 im einen Vektor wird dann mit dem Element an Position 1 im anderen Vektor gepaart, das Element an Position 2 im einen Vektor mit dem Element an Position 2 im anderen Vektor – und so weiter.

Werden ein ein-elementiger Vektor und ein mehr-elementiger Vektor mit einer Berechnung (etwa einer Addition) verknüpft, wird normalerweise das einzelne Element mit allen Elementen des anderen Vektors „gepaart“.

Wir werden nur diese Fälle betrachten: Entweder wird ein ein-elementiger Vektor mit einem längeren Vektor verknüpft oder zwei gleich lange Vektoren werden miteinander verknüpft. Es ist auch möglich, andere Kombinationen von Vektorlängen zu paaren, was wir jedoch erst einmal vernachlässigen; interessierte Leser können die folgenden Befehle in die R-Konsole eingeben und beobachten, was passiert.

2.2 Variablen

Wir wollen unsere Daten nicht nur in der Konsole ausgeben lassen, sondern auch abspeichern und damit arbeiten. Ein essentieller Bestandteil einer jeden Programmiersprache ist es, Daten in Variablen abzuspeichern. Variablen sind Namen, mit deren Hilfe wir auf gespeicherte Daten zugreifen. Wenn wir Daten in einer Variablen abgespeichert haben, können wir unter dem Namen der Variablen immer wieder darauf zugreifen. In R funktioniert das mit der Zuweisung <-.

Ich kann den Inhalt von Variablen in der R-Konsole ausgeben lassen, wenn ich den Namen der Variablen in die Konsole schreibe und Enter drücke:

[1]  1  2  6  7 10

Ich kann Variablen in Berechnungen verwenden:

[1]  2  4 12 14 20

Ich kann Funktionen auf Variablen anwenden und das Ergebnis der Funktion wiederum in einer Variablen speichern:

[1] -4.2 -3.2  0.8  1.8  4.8

Variablen können an jeder Stelle verwendet werden, an der man Daten sonst „händisch“ eingeben würde. Wir können jegliche Objekte – nicht nur Vektoren, sondern auch Datentabellen oder beliebig komplizierte Ergebnisse von Berechnungen – in Variablen speichern. Der Workflow in R ist so ausgelegt, dass Zwischenergebnisse weiterverwendet werden können. Hierbei unterscheidet es sich fundamental von SPSS, das einen Unterschied zwischen Daten und „Output“ macht. In R kann das Ergebnis jeglicher Berechnung als Input einer anderen Berechnung dienen.

Merke: In R kann (fast) alles in Variablen gespeichert und weiterverwendet werden.

Wir können auch mit einem Gleichzeichen = Daten zu Variablen zuweisen. Das funktioniert genauso wie mit <-:

[1] 1 2

In R hat sich aus historischen Gründen die Konvention durchgesetzt, <- zu verwenden, die ich in diesem Skript auch befolgen werde. In vielen anderen Programmiersprachen werden Variablen mit Gleichzeichen zugewiesen.

2.2.1 Ausgabe versus Abspeichern

Wir haben jetzt zwei verschiedene Möglichkeiten kennengelernt, Objekte6 in R zu verwenden:

  1. Wir geben Objekte in der Konsole aus.
  2. Wir speichern Objekte in einer Variable ab.

Diese beiden Verwendungen sind fundamental unterschiedlich. Das mag erst einmal trivial erscheinen, aber ist im Einzelfall nicht unbedingt ersichtlich. Betrachten wir das folgende Beispiel:

[1] -3  2  3  3  5  6  7  9

Die Funktion sort() sortiert den numerischen Vektor bar aufsteigend. Wie sieht der Vektor bar nach der Operation aus? Es gibt zwei Möglichkeiten:

  1. bar enthält den sortierten Vektor, den ich mithilfe von sort(bar) erstellt habe
  2. bar enthält den unsortierten Vektor, den ich vor der Operation sort(bar) erstellt habe

Wir können die Frage leicht klären, indem wir bar in der Konsole ausgeben:

[1]  3  2  6  3  9  5  7 -3

Offensichtlich hat sort(bar) den Vektor, der in der Variablen bar gespeichert ist, nicht geändert. Das ist eine fundamentale Eigenschaft der Programmiersprache R: Funktionen nehmen Daten an und sie geben Daten zurück – sie verändern aber nicht die eingegebenen Daten. Wenn wir wollen, dass bar die Zahlenfolge in sortierter Reihenfolge enthält, können wir die folgende Befehlkette verwenden:

In diesem Fall geht der Ursprungsvektor verloren und wir behalten nur den sortierten Vektor. Generell gilt: wenn wir Daten in der Konsole ausgeben lassen, verschwinden diese sozusagen im „Nirvana“. Wenn wir mit Daten weiterarbeiten wollen, müssen wir die Ausgabe einer Funktion in einer Variablen speichern. Beide Verwendungszwecke sind denkbar: Manchmal benötige ich nur die Ausgabe einer Berechnung, manchmal möchte ich das Ergebnis abspeichern.

2.2.2 Variablennamen

Generell bestehen Variablennamen aus Buchstaben und Zahlen und den Zeichen . und _. Folgende Einschränkungen sind zu beachten:

  • Variablennamen dürfen keine Leerzeichen enthalten
    • bla bla <- c(1, 2) funktioniert nicht
    • blabla <- c(1, 2) funktioniert
  • Variablennamen dürfen nicht mit einer Zahl starten
    • 1bla <- c(1, 2) funktioniert nicht
    • bla1 <- c(1, 2) funktioniert
  • Variablennamen dürfen keine Sonderzeichen außer _ oder . enthalten
    • bla-bla <- c(1, 2) funktioniert nicht
    • bla%bla <- c(1, 2) funktioniert nicht
    • bla_bla <- c(1, 2) funktioniert
    • bla.bla <- c(1, 2) funktioniert
  • bla <- 1 ist nicht das Gleiche wie Bla <- 1 oder gar BLA <- 1
  • Vermeidet Umlaute in Variablennamen. R wird diese zwar akzeptieren, aber ich würde dennoch davon abraten, sie zu nutzen.

Eine fundamentale Schwierigkeit beim Programmieren ist das Finden guter Variablennamen; bla und blabla sind denkbar schlechte Variablennamen. Gute Variablennamen sprechen, d.h. sie machen eine Aussage darüber, was für Daten sie beinhalten.

Beachtet immer folgende Regel: Variablennamen sollten nicht lügen, also verwendet niemals einen Namen der folgenden Art:

Man ist schnell geneigt einen unsinnigen Variablennamen zu vergeben, um keine Zeit mit der Namensfindung zu verschwenden – man hat ja schließlich wichtigen Code zu schreiben! Man sollte sich jedoch so gut wie immer kurz Zeit nehmen, einen sinnigen Namen zu finden – das zukünftige Selbst wird es einem danken. Unsinnige Variablennamen sind in Ordnung, wenn man sich zu 100% sicher ist, dass man die Variable nach einmaliger Nutzung nicht mehr verwendet. Wenn man eine Variable nicht mehr benutzen möchte, kann man sie mit der rm() Funktion löschen:

Weiterhin ist es guter Stil konsistent in der Vergebung der Variablennamen zu sein. Variablennamen sollen einen semantischen Gehalt haben, das heißt sie machen eine Aussage darüber, welche Daten sie enthalten. Häufig ist diese Information nicht in einem Wort erklärbar. Um auszusagen, dass eine Variable „das mittlere Alter“ enthält, müssen mindestens die Anteile „mittel“ und „Alter“ enthalten sein. Wie soll das verknüpft werden? Verschiedene Konventionen existieren; wichtig ist, dass ihr euch konsistent für eine Variante entscheidet.7

2.3 Datentypen von Vektoren

In R hat jeder Vektor genau einen Datentyp. Bis jetzt haben wir nur mit dem Datentyp Zahl gearbeitet, der in R „numeric“ heißt. Der Datentyp eines Vektors bestimmt, was für Operationen wir damit durchführen können. Vektoren vom Typ numeric etwa kann man addieren, multiplizieren und so weiter. Mit der Funktion mode können wir überprüfen, welchen Datentyp ein Vektor hat:

[1] "numeric"

In diesem Abschnitt werden weitere Datentypen behandelt, die wir nutzen, um unterschiedliche Informationen darzustellen.

2.3.1 character

Der Datentyp für Text heißt character. Text wird mit doppelten oder einfachen Anführungszeichen angegeben:

[1] "Hallo Welt!"

Mit Texten können wir andere Operationen durchführen als mit Zahlen, etwa ergibt Folgendes eine Fehlermeldung8 und ergibt auch gar keinen Sinn, da man Text nicht mit einer Zahl multiplizieren kann:

In erster Linie werden wir Vektoren vom Typ character für Datenzugriffe verwenden; im Speziellen werden wir sie einsetzen, um Spalten in Datentabellen zu adressieren, da Spalten normalerweise per Namen angesteuert werden (siehe Kapitel 3).

2.3.2 logical

Es hat sich als nützlich erwiesen, einen Datentyp einzuführen, der „Wahrheit“ kodiert. Dieser Datentyp wird in R “logical” genannt; er kennt nur die Ausprägungen TRUE und FALSE. Eine sonst gängige Bezeichnung für diesen Datentyp ist auch “boolean”.

Im Allgemeinen interpretieren wir TRUE/FALSE als logische Bedingungen, die entweder erfüllt sind oder nicht. Ist die Ampel grün? Hat die Versuchsperson eine Reaktionszeit von 2000ms oder mehr? Ist der Kuchen schon 60 Minuten im Ofen? Wir werden häufig vom Typ logical Gebrauch machen, wenn wir in Datentabellen Fälle auswählen; dann wird jeweils überprüft, welche Fälle die gewünschten Bedingungen erfüllen und anhand dessen findet eine Auswahl statt (etwa: wähle alle weiblichen oder männlichen Teilnehmer/innen in einer Umfrage aus).

Mit logischen Werten kann man die logischen Operationen UND (in R: & ), ODER (in R: | ) und NICHT (in R: ! ) umsetzen. UND und ODER verknüpfen jeweils zwei logische Bedingungen (sprich: zwei logische Werte, also TRUE/FALSE) miteinander und geben selbst einen logischen Wert zurück. UND gibt dann TRUE aus, wenn beide Bedingungen erfüllt sind, also nur dann, wenn die erste und die zweite Bedingung erfüllt ist:

[1] TRUE
[1] FALSE
[1] FALSE

ODER ist etwas weniger streng und gibt auch dann schon TRUE aus, wenn mindestens eine Bedingung erfüllt ist, also wenn die erste oder die zweite Bedingung erfüllt ist:

[1] TRUE
[1] TRUE
[1] FALSE

Beachtet, dass ODER immer TRUE ausgibt, wenn mindestens eine Bedingung erfüllt ist; also auch dann, wenn beide Bedingungen erfüllt sind – es ist kein umgangssprachliches entweder/oder.

Das logische NICHT invertiert die Eingabe: Aus TRUE wird FALSE und umgekehrt.

[1] FALSE
[1] TRUE

Die logischen Operationen UND und ODER arbeiten komponentenweise auf Vektoren, die mehr als ein Element enthalten:

[1]  TRUE FALSE FALSE
[1]  TRUE  TRUE FALSE

Auch das logische NICHT arbeitet vektorisiert. Es kann auf einen logischen Vektor angewendet werden, der beliebig viele Elemente enthält und kehrt alle Elemente darin um:

[1] FALSE  TRUE

Während die Operationen UND, ODER und NICHT an dieser Stelle nur abstrakt eingeführt werden, werden wir in weiteren Abschnitten (Kapitel 2 und Kapitel 3) noch lernen, wie wir logische Bedingungen verwenden, um gezielt Daten mit bestimmten Eigenschaften auszuwählen.

2.3.3 factor

Vektoren vom Typ factor stellen kategoriale Variablen dar – etwa die unabhängigen Variablen in einer Varianzanalyse. Mithilfe der Funktion factor() können wir einen Vektor vom Typ factor erstellen:

[1] :( :) :D :( :) :(
Levels: :( :) :D

Die Funktion factor() wandelt die numerischen Werte im Vektor laune in den Typ factor um. Das heißt: Den numerischen Kategorien (1, 2 und 3) in laune wird eine textuelle Beschreibung zugeordnet, hier umgesetzt durch unterschiedlich fröhliche Smileys. Es macht nur dann Sinn einen Vektor vom Typ factor anzulegen, wenn eine numerische Variable eine vordefinierte Zahl an Ausprägungen aufweist. Welche Ausprägungen im Eingangsvektor in diesem Fall möglich sind, habe ich mit dem zweiten Argument – 1:3 – spezifiziert.

Die Darstellung als factor ist für Menschen besser zu verarbeiten als numerische Kategorien. Die Bedeutung der numerischen Kodierung stellt eine Gedächtnisbelastung dar: War beispielsweise ein höherer Wert in laune besonders traurig oder besonders fröhlich? Ein Problem ist oftmals auch die Kodierung des Geschlechts von Studienteilnehmer*innen: Wurde weibliche Teilnehmerinnen jetzt mit einer 1 oder mit einer 2 kodiert? Bei einer Dateneingabe werden oftmals numerische Kodierungen eingegeben, da dies schneller geht als einen Text abzutippen. In der Datenauswertung sollten solche numerischen kategorialen Variablen jedoch immer in factor umgewandelt werden, damit die Kodierung eindeutig ist.

Mit einem Vektor vom Typ factor kann ich keine numerischen Berechnungen mehr durchführen, da er kategoriale Daten beinhaltet. Etwa kann ich für laune_faktor keinen Mittelwert berechnen:

[1] 1.666667
[1] NA

Da die Berechnung nicht möglich ist, gibt R folgende recht technisch klingende “Warnmeldung” aus:

In den meisten Fällen verhält sich ein Faktor wie ein Vektor vom Typ character und nicht wie ein numerischer Vektor (ein Beispiel dafür findet sich im Abschnitt Logische Vergleiche weiter unten). Inhaltlich macht das Sinn: In beiden Fällen ist das Vektorelement ein „Text“ – eine verbale Beschreibung. Der Unterschied ist, dass wir Faktoren normalerweise erhalten, indem wir eine numerische Kodierung in eine für Menschen verständliche verbale Beschreibung umwandeln.

2.3.4 NA

R hat einen eigenen Datentyp, um fehlende Werte zu kodieren: NA.9 Da wir mit echten Datensätzen arbeiten, die oftmals „messy“ sind, also nicht notwendigerweise vollständig, ist diese Eigenschaft sehr nützlich. Gerade bei der Arbeit mit Daten in der psychologischen Diagnostik ist das wichtig: Menschen geben in Fragebögen eben nicht immer auf alle Fragen eine Antwort.

Man kann selber Vektoren erstellen, die fehlende Werte enthalten:

Die Anwesenheit von fehlenden Werten hat Auswirkungen darauf, welche Berechnungen R mit dem Vektor anstellen kann. Etwa können wir nicht mehr ohne Weiteres einen Mittelwert berechnen:

[1] NA

Man muss R explizit mitteilen, dass man trotz des Auftretens fehlender Werte einen Mittelwert ausrechnen möchte. Dies funktioniert mit dem optionalen Argument na.rm10 der Funktion mean(), welches wir auf TRUE setzen können. Mit dem Argument na.rm (“NA remove”) teilen wir der Funktion mean() mit, dass fehlende Werte bei der Berechnung des Mittelwerts nicht berücksichtigt werden sollen. Ähnliche Funktionen wie sd() und var() nehmen auch das Argument na.rm an; andere Funktionen hingegen ignorieren fehlende Werte schon von Haus aus.

[1] 4.142857

Hierbei nehmen wir zur Kenntnis, dass man Argumente von Funktionen benennen kann (per “na.rm =”), was wir aber nicht immer machen. Zu diesem Thema mehr in Kapitel 3.

2.4 Logische Vergleiche

Wir können in R mithilfe von logischen Abfragen überprüfen, ob die Elemente in einem Vektor bestimmte Eigenschaften aufweisen. So können wir beispielsweise erfragen, welche Werte eines numerischen Vektors (a) gleich, (b) größer, (c) kleiner, (d) größer gleich, (e) kleiner gleich oder (f) ungleich einem bestimmten Wert sind. Der folgende Code-Abschnitt stellt die grundlegenden logischen Vergleiche für numerische Vektoren dar:

[1] FALSE FALSE FALSE  TRUE  TRUE
[1]  TRUE  TRUE FALSE FALSE FALSE
[1] FALSE FALSE  TRUE  TRUE  TRUE
[1]  TRUE  TRUE  TRUE FALSE FALSE
[1] FALSE FALSE  TRUE FALSE FALSE
[1]  TRUE  TRUE FALSE  TRUE  TRUE

Das Ergebnis dieser Operationen ist ein logischer Vektor aus TRUE und FALSE Werten. Die Werte nehmen TRUE an, wenn die Zahlen die kleiner/größer/gleich Bedingung erfüllen – andernfalls FALSE. Beachtet, dass auf Gleichheit mit dem “doppelten” == Operator getestet wird und nicht mit einem einfachen =. Dies ist eine häufige Quelle von Fehlern, die schwierig zu entdecken sind. Betrachtet etwa folgenden Code – was geht hier schief?

Hierbei wird die Variable daten mit dem Wert in der Variablen vergleichswert überschrieben, da = als Zuweisung agiert:

[1] 3

Dies ist ein Beispiel für einen Fehler (Bug), den man nicht anhand von einer Fehlermeldung bemerkt, da der Befehl syntaktisch korrekt ist. Es ist jedoch problematisch, dass ich an dieser Stelle meine Daten mit einem irrelevanten Wert überschrieben habe, und das bei einem späteren Zugriff darauf vermutlich nicht beachten werde.

2.4.1 Logische Vergleiche mit Vektoren vom Typ character

Welche logischen Vergleiche möglich sind, hängt vom Datentyp eines Vektors ab. Für Vektoren vom Typ character etwa macht eine Kleiner/Größer-Abfrage keinen Sinn, jedoch eine Abfrage auf Gleichheit:

[1] TRUE
[1] FALSE

Das funktioniert auch mit Vektoren vom Typ factor, die sich ja größtenteils wie Vektoren vom Typ character verhalten. Hier wird beim Test auf Gleichheit das überprüfte factor-Label in Anführungszeichen gesetzt:

[1] FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE

2.4.2 Komponentenweise Vergleiche

Wenn zwei Vektoren gleicher Länge mit logischen Operatoren verglichen werden, werden die Elemente komponentenweise verglichen:

[1] FALSE FALSE  TRUE FALSE FALSE  TRUE
[1] FALSE FALSE FALSE  TRUE FALSE FALSE

Erneut treffen wir auf dieses komponentenweise Verhalten. Wir können noch eine Schippe drauf legen, indem wir vektorisierte logische Vergleiche mit vektorisierten UND- oder ODER-Operationen verbinden:

[1] FALSE FALSE  TRUE FALSE  TRUE  TRUE

Es macht an dieser Stelle Sinn, darüber nachzudenken, wie diese Ausgabe zustande kommt.

2.4.3 Anwendungsbeispiel: Überprüfe das Gesetz der großen Zahlen

Häufig verwendet man die Vergleichsoperatoren, um zu prüfen, wie viele Daten eine bestimmte Eigenschaft erfüllen. Dafür können wir die Vergleichsoperatoren mit den Funktionen sum() oder mean() verknüpfen.

Dafür bietet sich ein Beispiel aus der Statistik an: Wie viele von 1,000 Zufallsdaten aus einer Standardnormalverteilung sind größer als 1? R hat zahlreiche Funktionen, um Zufallszahlen aus verschiedenen Verteilungen zu generieren. Mit rnorm() lassen sich Zufallszahlen generieren, die einer Normalverteilung folgen; wenn man keine weiteren Argumente angibt, ist die Standardnormalverteilung gemeint, die einen Mittelwert von 0 und eine Standardabweichung von 1 hat:

Zur Verdeutlichung: Der Vektor zufallsdaten enthält jetzt 1,000 Elemente, wie wir mit der Funktion length leicht überprüfen können:

[1] 1000

Die Funktion head() zeigt uns die ersten sechs Werte des Vektors an; sie ist sehr praktisch, um sich schnell einen Überblick über Daten zu verschaffen. Das machen wir hier auch, da wir nicht alle 1,000 Werte in die Konsole schreiben wollen:

[1]  1.3709584 -0.5646982  0.3631284  0.6328626  0.4042683 -0.1061245

Wir können die Daten mithilfe eines Histogramms betrachten, um uns davon zu überzeugen, dass sie tatsächlich normalverteilt sind – sich also der Großteil der Daten um die 0 tummelt und extreme Werte in beide Richtungen seltener werden (dieser Code muss nicht verstanden werden):

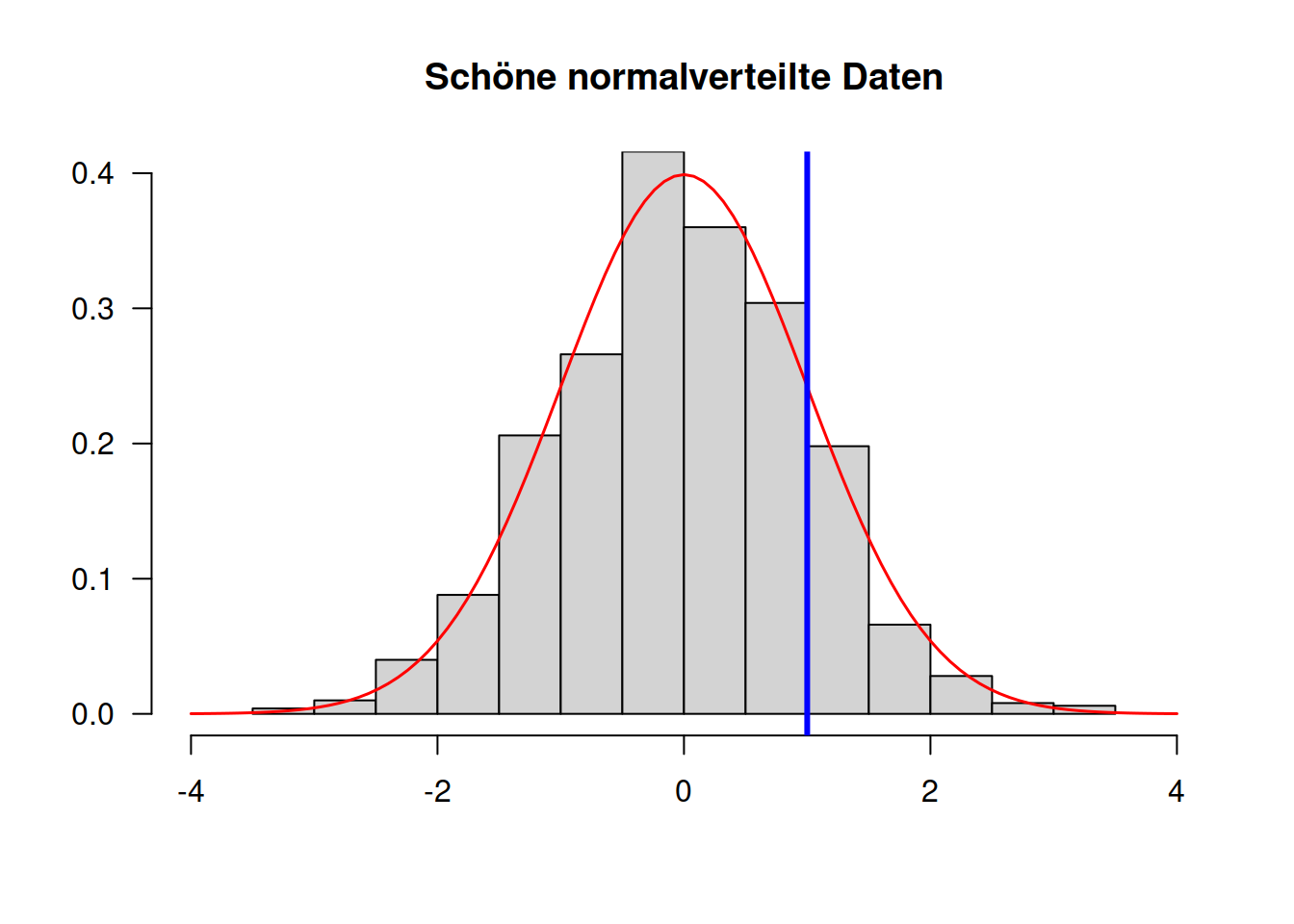
Nach visueller Inspektion der Verteilung der Zufallszahlen können wir mit sum testen, wie viele der 1,000 Zufallsdaten größer als 1 sind:

[1] 153

Zur Erinnerung: Der Befehl “zufallsdaten > 1” ergibt einen Vektor aus TRUE und FALSE Werten, der genauso viele Elemente enthält wie der Vektor zufallsdaten; wann immer ein Eintrag in zufallsdaten größer ist als 1, erhalten wir TRUE, andernfalls FALSE. Die Funktion sum() gibt die Zahl der TRUE Einträge aus. Das funktioniert, da TRUE und FALSE eine numerische Interpretation haben: TRUE wird als 1 interpretiert und FALSE als 0.11

Analog können wir mit mean() den relativen Anteil der Daten bestimmen, die größer als 1 sind:

[1] 0.153

Der Aufruf mean(zufallsdaten > 1) ergibt also den relativen Anteil der Datenpunkte, die größer sind als 1. Es lohnt sich ein wenig darüber nachzudenken, warum wir mean() hier verwenden können, um den relativen Anteil zu bestimmen. Normalerweise sind wir es eher gewohnt, dass Mittelwerte und relative Anteile etwas Unterschiedliches sind. Der Grund dafür ist folgender: Für eine Variable, bei der die Werte nur 1 oder 0 annehmen können (analog in R: TRUE/FALSE), entspricht der Mittelwert dieser Variablen dem relativen Anteil der Werte, die 1 bzw. TRUE sind. Als Beispiel betrachten wir den folgenden Vektor:

[1] 0.75

Der Mittelwert des Vektors ist (1 + 0 + 1 + 1) / 4, also 0.75 – und damit genau der relative Anteil der 1-Elemente. Dies ist eine praktische Eigenschaft der 1/0- bzw. TRUE/FALSE-Kodierung und macht logische Abfragen in R so mächtig.

Wenn wir einen relativen Anteil in eine Prozentzahl umwandeln wollen, können wir ihn einfach mit 100 multiplizieren:

[1] 15.3

Der Erwartungswert, dass eine zufällige Zahl aus einer Standardnormalverteilung größer ist als 1 – also mehr als eine Standardabweichung vom Mittelwert entfernt liegt – liegt bei etwa 15.9%. Den exakten Erwartungswert könnte ich in R mit der Funktion pnorm() herausfinden:

[1] 0.1586553

Die Funktion pnorm() ist die kumulative Verteilungsfunktion der Normalverteilung. Sie sagt aus, wie viel Prozent der Werte in einer Normalverteilung kleiner sind als der übergebene Wert. Um heraus zu finden, wie viele Werte größer als 1 sind, wird hier das Komplement, also 1 - pnorm(1), gebildet. Das funktioniert, da die Gesamtdichte einer Wahrscheinlichkeitsverteilung immer 1 ist.

Nach dem Gesetz der großen Zahlen liegt der folgende Wert wahrscheinlich näher am “wahren Wert” von 15.9% als der Schätzer, der auf 1,000 Zufallszahlen basiert:

[1] 0.15838

Ihr könnt für das Gesetz der großen Zahlen selber ein Gefühl entwickeln, wenn ihr mehrfach mean(rnorm(1000) > 1) und mean(rnorm(100000) > 1) in die R-Konsole eingebt und beobachtet, welcher Wert häufiger näher an 0.159 liegt.

2.4.4 Logische Operationen mit NA

Oftmals will man herausfinden, ob in Vektoren fehlende Werte vorliegen (also ob einige Elemente darin NA sind). Die Funktion is.na() führt eine logische Abfrage durch, die für jedes Element in einem Vektor überprüft, ob es NA ist.

[1] FALSE FALSE FALSE  TRUE FALSE  TRUE FALSE

Die Funktion is.na() gibt an den Positionen TRUE zurück, an denen in mein_vektor ein fehlender Wert vorliegt, ansonsten FALSE. Die Ausgabe ist also ein logischer Vektor, der genauso lang ist wie der Eingabevektor.

Oftmals kombiniert man is.na() mit der Funktion sum(), um die absolute Anzahl der fehlenden Werte zu erhalten:

[1] 2

Die Funktion mean() gibt dementsprechend die relative Häufigkeit fehlender Werte aus – die ist im Idealfall nicht allzu hoch.

[1] 0.2857143

Wichtig: Man muss is.na() verwenden, um zu prüfen, ob Werte in einem Vektor NA sind. Folgender „naiver“ Vergleich mit NA geht schief:

[1] NA NA NA NA NA NA NA

Auch bei Größer- oder Kleiner-Abfragen enthält sich R der Aussage, wie fehlende Werte zu klassifizieren sind. Dementsprechend wird im folgenden Befehl an den Positionen NA ausgegeben, an denen in mein_vektor ein Wert fehlt:

[1]  TRUE  TRUE  TRUE    NA FALSE    NA  TRUE

Ein logischer Vergleich mit NA ergibt immer NA, da beim fehlenden Wert keine Aussage darüber gemacht werden kann, ob er einem anderen Wert entspricht. Man kennt den fehlenden Wert zwar nicht, aber irgendeine Ausprägung hat er in der Realität.

Interessant ist auch der Umgang der UND- und ODER-Operationen mit fehlenden Werten. Der Befehl TRUE & NA gibt NA aus. Denn je nachdem, ob der fehlende Wert TRUE oder FALSE wäre, wäre das Ergebnis auch entweder TRUE oder FALSE. Wir können in diesem Fall nicht voraussagen, was das Ergebnis der UND-Operation wäre, da der fehlende Wert unbekannt, aber kritisch für das Ergebnis ist. Anders sieht es bei dem Befehl TRUE | NA aus. Dieser ergibt TRUE, da auf jeden Fall eine Bedingung erfüllt ist und nur eine Bedingung erfüllt sein muss, damit die ODER-Bedingung TRUE ergibt. Mit diesen Erklärungen im Hinterkopf können wir auch nachvollziehen, was passiert, wenn wir FALSE mit NA per UND und ODER verknüpfen: FALSE | NA ergibt NA, FALSE & NA ergibt FALSE.

2.4.5 Der %in%-Operator

Um zu testen, ob ein oder mehrere Elemente in einem Vektor enthalten sind, kann man den %in%-Operator verwenden. Der sieht zwar gewöhnungsbedürftig aus, ist aber einfach zu verwenden und hat auch eine einfache verbale Interpretation: Sind die Elemente aus Vektor A in Vektor B?

[1] TRUE
[1] FALSE

Wir können den %in%-Operator als eine Aneinanderreihung mehrerer ODER-Bedingungen verstehen. Folgendes ist äquivalent zu den obigen Aufrufen von %in%:

[1] TRUE
[1] FALSE

Der %in%-Operator ist wie so vieles in R „vektorisiert“, das heißt wir können für mehrere Elemente gleichzeitig testen, ob sie in einem Vektor enthalten sind:

[1] FALSE  TRUE

In diesem Fall wird für jedes der Vektorelemente vor %in% geprüft, ob dieses im Vektor nach %in% enthalten ist. Die Ausgabe der %in%-Operation ist immer ein logischer Vektor; die Länge des Ausgabevektors entspricht der Länge des Vektors auf der linken Seite von %in%.

2.5 Zugriff auf Vektorelemente

Der Zugriff auf Daten ist ein wichtiger Abschnitt unserer Einleitung in die Grundlagen von R. In diesem Abschnitt lernen wir, wie wir Elemente aus Vektoren „herausgreifen“ können und wie wir einzelne Elemente in einem Vektor ändern können. In Kapitel 3 wird als Fortführung behandelt, wie wir Daten aus Tabellen (wie wir sie etwa aus Excel kennen) auswählen können.

2.5.1 Der [·]-Zugriff

Daten können mit dem [·]-Zugriff12 indexbasiert aus Vektoren ausgewählt werden. Jedes Element im Vektor hat einen Index, der seiner Position im Vektor entspricht. Im folgenden Vektor etwa hat 2 den Index 1, 4 den Index 2 und 1 den Index 3:

Ich kann mit dem [·]-Zugriff durch Angabe des Index auf einzelne Elemente im Vektor zugreifen:

[1] 2
[1] 1

Ebenso kann ich einen „Negativ“-Zugriff durchführen: Ich kann auswählen, welchen Index ich nicht in meinem Ergebnis haben will:

[1] 4 1

Interessant wird diese Art des Zugriffs, da der Index in den [·] Klammern auch ein mehr-elementiger numerischer Vektor sein kann – hier nutzen wir die Funktion c():

[1] 2 4
[1] 2

2.5.2 [·]-Zugriff mit einem logischen Vektor

Anstatt direkt den Index eines Elements zu übergeben – den wir häufig nicht wissen, da wir bei vielen Daten nicht den Überblick über die Position aller einzelnen Datenpunkte behalten – möchten wir häufig Daten auswählen, die eine bestimmte Eigenschaft erfüllen. Hierbei machen wir uns die logischen Operationen zunutze, die wir oben kennengelernt haben:

[1] FALSE FALSE FALSE  TRUE  TRUE  TRUE

Der logische Vektor auswahl kodiert, welche Elemente des Vektors meinVektor größer sind als 5 (spezifisch: an welchen Positionen meinVektor ein Element enthält, das größer ist als 5). Ich kann nun auswahl in der [·]-Notation verwenden, um nur die Elemente auszuwählen, die größer sind als 5:

[1] 7 8 9

Hierbei wurden die Werte 7, 8 und 9 ausgewählt, da für diese Werte der Vektor auswahl auf TRUE steht. Genauer gesagt: auswahl steht für die Indexe 4, 5 und 6 auf TRUE und es gilt meinVektor[4] == 7, meinVektor[5] == 8, und meinVektor[6] == 9.

Man kann dieses Vorgehen sogar mit den UND/ODER-Operationen verknüpfen, um Daten anhand verschiedener Kriterien auszuwählen:

 [1]  TRUE  TRUE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[13] FALSE FALSE FALSE FALSE FALSE  TRUE  TRUE  TRUE
[1]  1  2  3  4 18 19 20

Hier ein weiteres Beispiel mit normalverteilten Zufallsdaten:

[1] 3.196362 2.386513 2.791331 2.123950

An dieser Stelle sollte man sich klar machen, warum daten sowohl vor als auch innerhalb der [·] Klammern vorkommt. Das ist prinzipiell dasselbe wie im Beispiel meinVektor[auswahl] oben, nur, dass ich dort den TRUE/FALSE Vektor, der die Daten ausgewählt hat, in einer Variablen – auswahl – zwischengespeichert habe.

2.5.3 [·]-Zugriff zum Ändern von Daten

Wir sind mit dem [·]-Zugriff nicht darauf beschränkt Elemente aus Vektoren auszulesen, sondern wir können auf diese Weise auch einzelne Elemente im Vektor verändern:

[1] 1 0 3 4 0

Dies geht wiederum auch mit einem logischen Vektor in den [·]-Klammern, wie das folgende Beispiel zeigt:

[1] 0 2 0 4 5

Das würde man so “händisch” nicht machen, aber es soll zum Verständnis dessen dienen, was im folgenden – anwendungsnäheren – Beispiel passiert. Angenommen, bei einer Dateneingabe wurden fehlende Werte in einem Fragebogen mit -99 kodiert.13 Wir wollen R mitteilen, diesen Wert als fehlend zu interpretieren. Hier kommt uns wiederum eine logische Abfrage zugute:

 [1]   1 -99   5 -99   2 -99   4   1   2   3
 [1] FALSE  TRUE FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE FALSE

Die Variable missing_values kodiert jetzt, an welchen Positionen des Vektors daten sich eine -99 befindet. Wir können diese Werte nun wie folgt durch NA ersetzen:

 [1]  1 NA  5 NA  2 NA  4  1  2  3

Semantisch ist dieser Vorgang gut zu verstehen: Setze alle Werte, die einen fehlenden Wert enthalten – d.h. mit -99 kodiert wurden – auf NA, damit R für weitere Berechnungen weiß, dass diese Werte als fehlend zu verstehen sind. Technisch umgesetzt wird dies mit einem TRUE/FALSE Vektor, den wir mithilfe der Anweisung daten == -99 erstellt haben.

Wir werden wohl selten “händisch” per Index oder logischem TRUE/FALSE Vektor eine Auswahl/Änderung von Daten durchführen. Aber in Zusammenarbeit mit den logischen Operatoren (>, <, ==, &, | etc.) ist die Auswahl von Elementen aus Vektoren – und auch die Auswahl von Daten aus Tabellen – eine häufige Anwendung. Diese werden wir bei der gezielten Auswahl von Zeilen aus Datentabellen (siehe Kapitel 3) wiederfinden und uns zunutze machen. Das gegebene Beispiel zur Umkodierung von fehlenden Werten werden wir in einer sehr ähnlichen Form in Kapitel 5 nutzen, da wir sonst Daten aus dem Narcissistic Personality Inventory nicht auswerten können. Bevor die Analyse startet, müssen fehlende Werte gekennzeichnet werden.

2.6 Präzedenz

Durch Klammerung können wir die Präzedenz von R-Befehlen steuern. Präzendenz bezieht sich auf die Reihenfolge, in der R-Befehle ausgeführt werden. Betrachten wir das folgende Beispiel:

[1] TRUE

Die Ausgabe ist TRUE. Daraus können wir schlussfolgern, dass die Befehle ODER und UND nicht von links nach rechts ausgeführt wurden. In dem Fall wäre nämlich zunächst TRUE | TRUE ausgeführt worden, was TRUE ergibt. Dieses Ergebnis (also TRUE) wäre dann per UND mit FALSE verknüpft worden, was insgesamt FALSE ausgegeben hätte. Wir haben aber TRUE bekommen. Warum?

Der Grund: Die UND-Operation hat eine höhere Präzedenz als die ODER-Operation. Wenn UND und ODER in einem logischen Ausdruck verbunden werden, wird zunächst die UND und dann die ODER-Operation ausgeführt, unabhängig davon, in welcher Reihenfolge wir die Befehle aufschreiben. Möchten wir erzwingen, dass die ODER-Operation zuerst durchgeführt wird, können wir – ganz analog zu mathematischen Berechnungen – Klammern verwenden:

[1] FALSE

Die Präzendenzregeln gelten ebenfalls, wenn die logischen Vektoren aus mehr als einem Element bestehen. Betrachten wir dazu die folgenden Beispiele:

[1] FALSE  TRUE
[1] FALSE FALSE

Wir werden logische Ausdrücke vor allem zur Fallauswahl in Datentabellen verwenden (siehe Kapitel 3). Dann kann es sehr wichtig sein, auf korrekte Klammerung zu achten. Andernfalls besteht die Gefahr, dass wir nicht genau die Fälle auswählen, die wir eigentlich auswählen wollen.

Betrachten wir ein weiteres Beispiel zur Steuerung von Präzedenz: Nehmen wir an, wir benötigen eine Sequenz aller Zahlen zwischen 1 und 10 – außer der 8.14 Ein naheliegender Befehl wäre folgender:

 [1]  1  2  3  4  5  6  7  8  9 10

Das hat aber nicht funktioniert, die Acht ist in der Ausgabe enthalten. Woran liegt das? Die Auswahl per eckiger Klammer hat eine höhere Präzedenz als der Doppelpunktoperator. Die Klammerungsoperation zur Auswahl aus einem Vektor wurde also nicht auf den Vektor 1:10, sondern auf den Vektor 10 angewendet (Erinnerung: Einzelne Zahlen sind Vektoren). Das heißt, in diesem Beispiel wurde als Erstes das achte Element aus dem Vektor 10 ausgeschlossen, das aber gar nicht existiert. Stattdessen erhalten wir einfach wieder 10:

[1] 10

Durch Klammerung können wir das gewünschte Ergebnis erhalten:

[1]  1  2  3  4  5  6  7  9 10

Merke: Im Zweifel verwenden wir Klammern lieber einmal zu viel als einmal zu wenig.

2.7 Zusammenfassung

  • Wir haben die grundlegendste Datenstruktur von R, den Vektor, kennengelernt
  • Vektoren enthalten beliebig viele Elemente gleichartiger Daten, etwa
    • Zahlen (“numeric”)
    • Texte (“character”)
    • Kategorielle Daten (“factor”)
    • TRUE/FALSE (“logical”)
  • Mit dem [·]-Zugriff kann man Elemente aus Vektoren auswählen
    1. indem man die Position der Elemente angibt, die man auswählen will (“Positivauswahl”)
    2. indem man die Position der Elemente angibt, die man nicht auswählen will (“Negativauswahl”)
    3. indem man einen TRUE/FALSE Vektor angibt
  • Man kann mit logischen Vergleichen die Eigenschaften von Vektoren überprüfen
    • diese Operation lässt sich gut mit der [·]-Auswahl verbinden

2.8 Fragen zum vertiefenden Verständnis

  1. Wie berechnet man den Standardfehler von 1:10?
  2. Was für Objekte nimmt die Funktion c() entgegen, und was gibt sie zurück?
  3. Was ergibt 1:6 + 1:2? Was passiert? Warum gibt 1:4 + 1:3 eine Warnmeldung aus?
  4. Nutzt paste0(), den :-Operator und den [·]-Negativ-Zugriff, um den folgenden Vektor zu erstellen:
[1] "item_2"  "item_4"  "item_5"  "item_6"  "item_7"  "item_8"  "item_10"
  1. In R haben Elemente eines Vektors nur einen Datentyp. Der Befehl c(1, 'moep') vermischt eine Zahl und einen Text miteinander, aber ergibt keinen Fehler – was ist passiert?
  2. Was sind plausible Ergebnisse von sum(rnorm(100) > 1.645)? (Erst überlegen, dann mehrfach in der R-Konsole ausführen!)
  3. Was sind die Ausgaben von mode(2) und mode(mode(2)). Warum?
  4. Was ist der Unterschied zwischen sum(c(TRUE, FALSE, TRUE)) und length(c(TRUE, FALSE, TRUE))?

  1. Interessanterweise gibt es sogar Vektoren der Länge 0 – also Vektoren, die gar kein Element beinhalten. Das soll uns aber erst einmal nicht beschäftigen.↩

  2. R würde oft auch bei einelementigen Vektoren ein Ergebnis ausgeben, aber das ist zum Beispiel beim Mittelwert wenig sinnvoll.↩

  3. Bis jetzt kennen wir nur das Vektor-Objekt. In R gibt es aber ganz verschiedene „Datencontainer“, die allgemein als Objekte bezeichnet werden.↩

  4. Ich werde von dieser Regel in diesem Skript abweichen.↩

  5. Leider sind Fehlermeldungen in R oftmals sehr kryptisch und gerade für Anfänger schwer verständlich.↩

  6. Eigentlich ist NA kein eigener Datentyp. In R hat jeder Vektor nur genau einen Datentyp. Es ist beispielsweise nicht möglich, dass in einem Vektor gleichzeitig Werte vom Typ numeric, character und factor vorkommen. NA-Werte können jedoch in Kombination mit jedem Datentyp vorkommen. Sie kodieren dann die Abwesenheit eines Datums; dieses Datum hätte – wenn es nicht fehlen würde – den Datentyp des Vektors.↩

  7. Ein Argument heißt optional, wenn wir dafür keinen Wert angeben müssen. Stattdessen hat es einen sogenannten Standardwert, der angenommen wird, wenn wir das Argument nicht selber angeben. Der Standardwert des Arguments na.rm der Funktion mean() ist FALSE.↩

  8. Wenn logische Vektoren einer numerischen Berechnung übergeben werden, werden die TRUE/FALSE Elemente des Vektors automatisch in Zahlen, d.h. 1 und 0 umgewandelt. Deswegen funktioniert beispielsweise auch folgender Befehl: TRUE + 1↩

  9. Ich nenne diese Operation [·]-Zugriff , da zur Datenauswahl aus Vektoren hinter den Vektor eckige Klammern gestellt werden. Die Klammern enthalten eine Angabe darüber, welche Elemente ich aus dem Vektor auswählen will. Etwa wählt c(4, 2, 6)[1] das erste Element aus dem Vektor c(4, 2, 6) aus, also 4. Der Punkt ist bloß ein Platzhalter in der [·]-Notation.↩

  10. Das macht beispielsweise Sinn, damit bei der Eingabe explizit gemacht wird, dass der Wert fehlt. Andernfalls könnte das Datum bei der Eingabe auch vergessen worden sein.↩

  11. Das Beispiel mag hier künstlich wirken, aber genau so etwas werden wir in Kapitel 4 machen.↩