6 Funktionen

Funktionen sind das Herz der R-Maschinerie. Jegliche Befehle, die wir in R durchführen, sind als Funktionen umgesetzt.31 Wir haben bereits ausgiebig von Funktionen Gebrauch gemacht. Wir haben beispielsweise mit subset() Daten ausgewählt, mit table() und tapply() deskriptive Statistiken angefordert, und mit cor(), colMeans() und psychometric::alpha() psychometrische Berechnungen durchgeführt. Dabei haben wir bereits einige Eigenschaften von Funktionen zur Kenntnis genommen, etwa dass sie Namen haben,32 Argumente annehmen und ihre Rückgabewerte in Variablen gespeichert werden können. In diesem Kapitel soll nun ein tiefgründigerer Blick auf Funktionen in R gelegt werden. Am Ende des Kapitels lernen wir, unsere eigenen Funktionen zu schreiben.

6.1 Das Black-Box-Modell

Diese Grafik zeigt schematisch die Arbeitsweise von R-Funktionen:

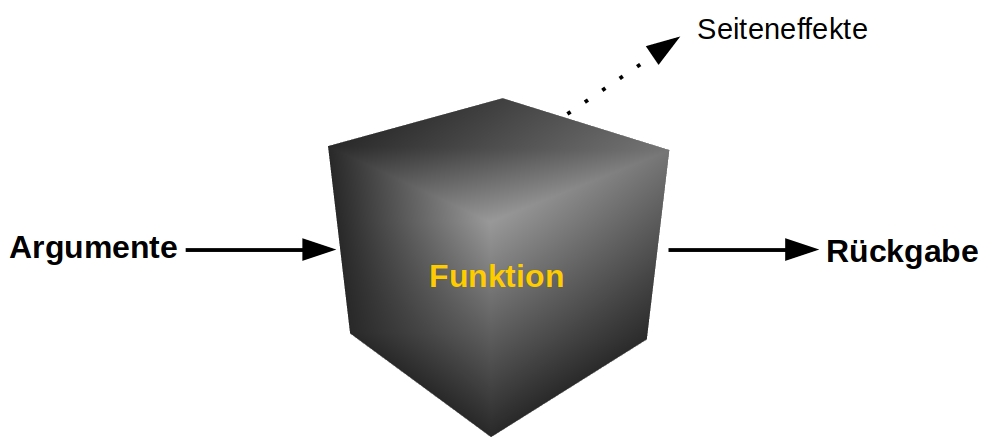
Funktionen nehmen Argumente an, die ihr Verhalten steuern. Sie geben genau ein R-Objekt zurück, das Rückgabewert genannt wird. Wenn der Aufruf einer Funktion außer dieser Rückgabe weitere Auswirkung auf die „Umgebung“ hat, nennt man das einen Seiteneffekt. Als R-Neuling ist es manchmal wichtig zu verstehen, was der Unterschied zwischen den Seiteneffekten und der Rückgabe einer Funktion ist.

Die innere Arbeitsweise von Funktionen wird als „Black Box“ betrachtet. Wir wissen nicht unbedingt, wie eine Funktion intern funktioniert, was uns aber auch nicht interessiert. So lange uns mean() den korrekten Mittelwert ausgibt, ist uns egal, wie mean() den Mittelwert berechnet.33 Bei Funktionen interessiert uns in erster Linie, welche Daten wir einer Funktion als Argumente übergeben müssen und was sie uns dafür in Austausch zurückgeben. Die folgenden Abschnitte befassen sich mit den einzelnen Bestandteilen des „Black-Box-Modells“.

6.2 Argumente

Argumente determinieren das Verhalten von Funktionen. Im einfachsten Fall bedeutet das, dass die Elemente eines Vektors, den wir mean() übergeben, den ausgegebenen Mittelwert determinieren. Wenn wir gar keinen Vektor übergeben, erhalten wir kein Ergebnis, sondern eine Fehlermeldung:

Um zu verstehen, wie man mit Argumenten das Verhalten von Funktionen beeinflusst, ist ein Verständnis der folgenden Punkte wichtig:34

  1. Manche Argumente haben Standardwerte (Englisch: „default values“), die angenommen werden, wenn wir diese Argumente beim Aufrufen der Funktion nicht explizit angeben. Diese Argumente heißen optionale Argumente.
  2. Wenn Argumente keinen Standardwert haben, müssen wir dem Argument einen Wert übergeben, da die Funktion sonst eine Fehlermeldung und kein Ergebnis ausgibt.35
  3. Argumente haben Namen, die wir verwenden können, um sie in der Form Argumentname = Wert zu adressieren.
  4. Wenn wir für ein Argument nicht explizit den Namen angeben, wird das Argument nach seiner Position in der Liste aller angegeben Argumente identifiziert.
  5. Mit der R-Hilfe können wir herausfinden, welche Argumente Funktionen annehmen, wie diese heißen, und welche davon optional oder verpflichtend sind.

Wir werden diese Punkte nun exemplarisch anhand der Funktion mean() nachvollziehen. Wir wissen bereits, dass mean() mindestens zwei Argumente annimmt. Beide Argumente haben Namen:

  • x: der numerische oder logische Vektor, für den der Mittelwert bestimmt werden soll. Oftmals wird in R das „Datenargument“ (das zumeist das erste Argument ist) generisch mit x benannt.
  • na.rm: ein ein-elementiger logischer Vektor, der angibt, ob NA-Werte von der Berechnung ausgeschlossen werden sollen

Da der Aufruf mean() ohne Angabe eines numerischen oder logischen Vektors einen Fehler ergibt, ist uns klar, dass x kein optionales Argument ist. Wir müssen einen Vektor übergeben, für den wir einen Mittelwert bestimmen können. Wieso mean() auch sonst aufrufen?

Auf der anderen Seite wissen wir auch, dass wir das Argument na.rm nicht unbedingt angeben müssen – das würden wir normalerweise nur dann machen, wenn wir wissen, dass unsere Daten fehlende Werte enthalten. Folgender Aufruf funktioniert nämlich, ohne dass wir dem Argument na.rm einen Wert übergeben:

[1] 5.5

Doch was passiert mit na.rm, wenn wir es nicht explizit angeben? Hierbei nehmen wir folgende Regel zur Kenntnis: Optionale Argumente sind deswegen optional, da ihnen von der Funktion ein Wert zugewiesen wird, wenn wir das Argument nicht selbst übergeben. Das Argument na.rm hat den Standardwert FALSE, weswegen NA-Werte im Normalfall nicht von der Berechnung ausgeschlossen werden. Stattdessen wird uns NA zurückgegeben, wenn x mindestens einen fehlenden Wert enthält. Folgende Aufrufe sind demnach äquivalent:

Da wir nicht immer alle optionalen Argumente von Funktionen angeben wollen – stattdessen „vertrauen“ wir auf die Standardwerte –, ist es sehr hilfreich, dass wir Funktionsargumente per Namen ansprechen können. So können wir nur genau die optionalen Argumente auswählen, die wir anpassen wollen; für die anderen belassen wir den Standardwert.

Interessanterweise wissen wir bislang gar nicht, ob wir das Argument na.rm tatsächlich mit Namen ansteuern müssen. In Funktionen können wir Argumente ja anhand ihres Namens oder ihrer Position ansprechen. Wenn na.rm das zweite Argument wäre, könnten wir auch folgenden Aufruf verwenden:

Das hat aber nicht funktioniert. Diese Fehlermeldung informiert uns darüber, dass mean an der zweiten Position ein Argument mit dem Namen „trim“ erwartet. Offensichtlich hat mean mit trim noch ein weiteres optionales Argument, das wir bislang gar nicht kannten. Das heißt für uns: Solange wir für trim – was auch immer das ist – keinen Wert angeben, müssen wir na.rm per Namen ansprechen.

Wenn wir Argumente mit Namen ansteuern, brauchen wir uns über die Reihenfolge der Argumente keine Gedanken machen. Das ist oftmals sehr hilfreich. Deswegen funktioniert folgender Aufruf:

[1] 5.5

Wir erweitern nun das Beispiel von oben unter Berücksichtigung unseres Wissens über die Vergabe von Namen bei Funktionsargumenten. Folgende Aufrufe sind alle äquivalent:

Nicht äquivalent zu den obigen Aufrufen sind jedoch folgende Befehle, die zu Fehlermeldungen führen, da na.rm nicht das zweite Argument von mean() ist:

Wir haben nun gelernt, wie wir Argumente an Funktionen übergeben können. Dieses Wissen hilft uns jedoch nur, wenn wir folgende Frage beantworten können:

Wie finden wir heraus, welche Argumente eine Funktion annimmt?

6.2.1 Die R-Hilfe

In R sind bereits sehr viele statistische und testtheoretische Analysen als Funktionen verfügbar. Wenn diese Funktionen noch nicht in der Basisversion von R enthalten sind, sind sie stattdessen häufig in externen Paketen verfügbar. So können wir beispielsweise ANOVAs, explorative oder konfirmatorische Faktorenanalysen und viele andere Auswertungen durchführen – wenn wir denn wollen. Wir benötigen dabei nur das folgende Wissen:

  1. Welche Funktion führt die gewünschte Berechnung aus?
  2. Wie können wir diese Funktionen bedienen?

Wir beschäftigen uns im Folgenden mit dem zweiten Punkt.36 Wir lernen, wie wir uns mit der R-Hilfe einen Überblick über die Arbeitsweise von Funktionen verschaffen können. Probieren wir es exemplarisch für die Funktion mean() aus:

Interessant ist für uns erst einmal der obere Abschnitt „Usage“:

Wir ignorieren an dieser Stelle, dass uns zwei Varianten angeboten werden, die Funktion mean() zu nutzen.37 Wenn in der Hilfe eine „Default S3 method“ angeboten wird, interessiert uns oftmals diese; so ist es auch hier der Fall. An dieser Stelle finden wir die Informationen, die wir benötigen, um die Funktion zu nutzen. Wir sehen

  • die Namen der Argumente
  • die Reihenfolge der Argumente
  • welche Argumente optional sind
  • was die Standardwerte der optionalen Argumente sind

Die Standardwerte der optionalen Argumente lassen sich dadurch ablesen, dass in der Argumentliste in der Form Argumentname = Wert schon ein Wert angegeben ist. Das Argument trim etwa hat den Standardwert 0. Wie wir bereits wissen, hat das Argument na.rm den Standardwert FALSE. Bei nicht-optionalen Argumenten ist kein Standardwert, sondern nur der Name des Arguments angegeben.

Wenn wir mehr über die Argumente erfahren wollen, müssen wir den Abschnitt „Arguments“ der R-Hilfe konsultieren. Folgende Punkte interessieren uns bei der Beschreibung:

  1. Was ist die inhaltliche Bedeutung eines Arguments?
  2. Was für ein R-Objekt muss ich übergeben, um ein Argument anzusteuern? (Z.B. einen Vektor, einen data.frame, eine matrix, eine list oder sogar eine Funktion – siehe Kapitel 3: Funktion tapply)

Die Beschreibung der Argumente achtet sehr auf Prägnanz und technische Korrektheit, wie wir am Beispiel der Beschreibung der Argumente der Funktion mean erkennen können:

Die R-Hilfe ist also hilfreich, aber nicht immer ganz leicht zu nutzen. Oftmals ist eine weitere Google-Recherche oder das Nachfragen bei einer Freundin oder einem Freund sinnvoll, wenn man die Nutzung einer Funktion meistern will.

Mehr Hilfe zur Nutzung einer Funktion finden wir im Abschnitt „Examples“ der R-Hilfe. Hier können wir am konkreten Beispiel betrachten, wie die Funktion angewendet werden kann. Wenn wir Glück haben, ist genau das dabei, was wir brauchen. Der Code ist dabei so gewählt, dass man ihn per Copy & Paste einfach selbst in der Konsole ausführen kann. Bei mean() finden wir etwa den folgenden Beispiel-Code:

Hinweis: Wenn die R-Hilfe nicht so hilfreich ist, schaut euch die Beispiele an.

6.2.2 Namenlose Argumente

In der Einführung in die Arbeitsweise von Funktionsargumenten habe ich behauptet, dass Argumente Namen haben. Wie fast jede allgemeine Regel hat auch diese Regel Ausnahmen – Argumente haben nämlich gar nicht immer einen Namen. Das ist für uns zwar nicht ganz so wichtig, aber wir können es hier zur Kenntnis nehmen. Wir haben sogar schon mit Funktionen gearbeitet, die namenlose Argumente annehmen können. Das ist beispielsweise immer dann notwendig, wenn Funktionen eine beliebige Anzahl von Argumenten annehmen. Die Funktion c nimmt beliebig viele Vektoren entgegen, die dann zu einem Vektor zusammengefügt werden. Auch andere Funktionen wie table() – die beliebig viele Vektoren zur Erstellung von Kreuztabellen annimmt – und dplyr::arrange() – die beliebig viele Kriterien zur Sortierung eines data.frames annimmt – haben unbenannte Argumente. In der R-Hilfe ist dies oftmals an dem Platzhalterargument „...“ (lies: ellipsis) zu erkennen, siehe:38

6.3 Rückgabewerte

Der Rückgabewert einer Funktion ist das R-Objekt, das die Funktion ausgibt. Jede Funktion hat einen Rückgabewert. Die Funktion mean() gibt beispielsweise einen ein-elementigen Vektor aus, der das arithmetische Mittel des Eingabevektors repräsentiert. Die Funktion subset() gibt immer einen data.frame aus – wie der aussieht, bestimmen die Argumente, die wir der Funktion übergeben.

Das Verständnis von Rückgabewerten führt uns etwas tiefer in die Innereien der R-Programmiersprache. Betrachten wir im folgenden Beispiel die Funktion t.test(), die einen t-Test durchführt und dabei die Mittelwerte zweier Vektoren vergleicht. Ich verwende den NPI-Datensatz aus Kapitel 5 und vergleiche den mittleren Narzissmus-Gesamtwert (Spalte score) zwischen weiblichen und männlichen Testnehmenden (Spalte gender; Kodierung: männlich = 1, weiblich = 2).39

Wir erhalten folgende Ausgabe in der Konsole:


    Welch Two Sample t-test

data:  npi$score[npi$gender == 1] and npi$score[npi$gender == 2]
t = 13.249, df = 10681, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 1.801341 2.426906
sample estimates:
mean of x mean of y 
 14.19595  12.08183

Hier werden uns alle relevanten Aspekte der t-Test-Berechnung ausgegeben. Ein erster interessanter Hinweis ist, dass kein klassischer t-Test, sondern ein „Welch Two Sample t-test“ gerechnet wurde.40 Weiterhin werden uns t-Wert, Freiheitsgrade, p-Wert („p-value < 2.2e-16“ bedeutet, dass der p-Wert so klein ist, dass vor dem ersten Wert hinter dem Komma, der nicht Null ist, mindestens 16 Nullen stehen), das 95%-Konfidenzintervall der Differenz der mittleren Werte, sowie die Mittelwerte selbst ausgegeben. Insgesamt kann man interpretieren, dass Männer im Mittel signifikant höhere Narzissmuswerte aufweisen als Frauen. Aber dieser Befund ist für uns in diesem Fall uninteressant – wir wollen uns ja mit dem Rückgabewert befassen. Was für ein R-Objekt wurde uns denn ausgegeben?

Was in der Konsole angezeigt wird, stellt nicht direkt das R-Objekt dar, das die Funktion t.test() ausgibt. Es handelt sich hierbei um eine etwas lesefreundlichere Zusammenfassung des Tests. Um das tatsächlich ausgegebene Objekt zu inspizieren, kann ich die Funktion str() verwenden. Dazu speichere ich die Ausgabe des t-Tests zunächst in einer Variablen ab:

List of 10
 $ statistic  : Named num 13.2
  ..- attr(*, "names")= chr "t"
 $ parameter  : Named num 10681
  ..- attr(*, "names")= chr "df"
 $ p.value    : num 9.4e-40
 $ conf.int   : num [1:2] 1.8 2.43
  ..- attr(*, "conf.level")= num 0.95
 $ estimate   : Named num [1:2] 14.2 12.1
  ..- attr(*, "names")= chr [1:2] "mean of x" "mean of y"
 $ null.value : Named num 0
  ..- attr(*, "names")= chr "difference in means"
 $ stderr     : num 0.16
 $ alternative: chr "two.sided"
 $ method     : chr "Welch Two Sample t-test"
 $ data.name  : chr "npi$score[npi$gender == 1] and npi$score[npi$gender == 2]"
 - attr(*, "class")= chr "htest"

Das von t.test() ausgegebene Objekt ist eine „List of 9“, also eine Liste mit 9 Einträgen. Listen sind sehr allgemeine Datencontainer, die Elemente von beliebigem Typ und beliebiger Anzahl beinhalten können.41 Listen stellen eine wichtige Datenstruktur in R dar – vielleicht ist es sogar die wichtigste Datenstruktur, da data.frames spezielle Listen sind, in denen jeder Eintrag (d.h., jede Spalte) ein Vektor gleicher Länge ist. Die Elemente der Liste können benannt sein, wie es bei der Rückgabe von t.test() der Fall ist. In diesem Fall kann ich, wie wir es von der Spaltenauswahl in data.frames kennen, mit der $-Notation auf einzelne Elemente zugreifen:

       t 
13.24906 
[1] "two.sided"
     df 
10681.4

Es ist nicht unüblich, dass komplexere statistische Berechnungen eine Liste als Ausgabeobjekt ergeben. Listen sind dann sinnvoll, wenn während der Berechnung mehrere Werte anfallen und es nützlich ist, diese an den Nutzer zurückzugeben. Im Falle des t-Tests interessieren uns etwa die Freiheitsgrade, der t-Wert und der p-Wert.

6.4 Seiteneffekte

Jede Funktion hat genau einen Rückgabewert, also genau ein R-Objekt, das von der Funktion zurückgegeben wird. Jegliche Auswirkungen, die eine Funktion darüber hinaus hat – außerhalb der inneren Arbeitsweise –, werden Seiteneffekte genannt. Beispielsweise war die Konsolen-Ausgabe der Funktion t.test() im oberen Fall ein Seiteneffekt. Wenn ich die Funktion t.test() aufrufe, wird mir eine Zusammenfassung des Tests in der Konsole ausgeben, die als Mensch etwas einfacher zu verarbeiten ist als die Liste, die die „tatsächliche“ Rückgabe darstellt. Das Zeichnen von Abbildungen ist auch als Seiteneffekt zu verstehen. Wenn wir beispielsweise hist(npi$score) aufrufen, wird uns ein Histogramm der Narzissmuswerte des NPI angezeigt. Dieses Histogramm ist ein Seiteneffekt und nicht die Ausgabe der Funktion hist(). Interessierte sind aufgefordert herausfinden, was deren tatsächliche Rückgabe ist.

Ich werde die Diskussion von Seiteneffekten bei dieser kurzen und oberflächlichen Einführung belassen. Manchmal ist die Unterscheidung in Seiteneffekte und Rückgabe sinnvoll; wenn wir etwa die Ergebnisse einer Funktion weiter verwenden möchten, ist es wichtig zu wissen, welche Datenstruktur die Funktion ausgibt und wie wir auf die ausgegebenen Werte zugreifen können. Um Power-Analysen für t-Tests zu simulieren, ist es beispielsweise nötig, die exakten p-Werte aus der Ausgabe der Funktion t.test() auszulesen. In dem Fall werden wir die Funktion t.test() gegebenenfalls 10,000 Mal aufrufen und können es uns nicht leisten, den p-Wert jedes Mal aus der Konsolen-Ausgabe abzulesen. Stattdessen wollen wir den Prozess der p-Wert-Extraktion automatisieren; und genau für solche Automatisierungen lernen wir das Programmieren.

6.5 Selbst geschriebene Funktionen

Das Schreiben eigener Funktionen sollte früher oder später zum Repertoire eines R-Nutzers gehören. Mit selbst geschriebenen Funktionen können wir häufig durchgeführte Berechnungen abstrahieren und beliebig oft durchführen. Betrachten wir den folgenden Code:

Erkennt ihr, was berechnet wird? Falls nicht, betrachtet diesen Code:

In der ersten Variante sind nur ein paar Zahlen und arithmetische Operationen zu sehen, die Semantik der Berechnung ist jedoch vollkommen unklar. Durch das Copy-Pasten des Codes ist mir sogar ein Fehler unterlaufen, denn ich habe in der zweiten Zeile einmal vergessen den Wert 0.23 durch 0.47 auszutauschen – solche Fehler passieren häufig und sind sehr schwierig zu entdecken (siehe Li, Lu, Myagmar, & Zhou, 2006). Durch die Nutzung der Funktion, die ich in Kapitel 5 definiert habe, ist der Code lesbarer geworden und einfach interpretierbar: Ich möchte drei Reliabilitätsschätzer um die Faktoren 2, 3 bzw. 4 korrigieren. Sofern ich bei der Definition meiner Funktion keinen Fehler gemacht habe, sind diese Aufrufe auch robuster gegenüber Copy-Paste-Fehlern.

Mit eigenen Funktionen folgen wir dem Programmierer-Credo „do not repeat yourself“. Wenn wir einmal Code zur Lösung eines Problems geschrieben haben, möchten wir denselben Code nicht noch einmal schreiben, um ein gleiches bzw. ähnliches Problem zu lösen. Eigene Funktionen helfen uns effizienter – man könnte sogar sagen: fauler – zu arbeiten. Außerdem führen sie zu besser lesbarem Code, denn Funktionsnamen42 kommunizieren die Intention von Code deutlich besser als das reine Aneinanderreihen von Zahlen, Operatoren und Variablen.

6.5.1 Definition der eigenen Funktion

Erinnern wir uns an die Spearman-Brown-Funktion, die ich in Kapitel 5 definiert habe:

Um die Funktion zu definieren, führe ich diese sechs Zeilen Code einfach in der R-Konsole aus. In RStudio reicht es sogar, STRG-Enter zu drücken, wenn sich mein Cursor in Zeile 1 befindet. In dieser Zeile beginnt die Definition der Funktion: Ich erstelle eine Variable, der ich mit „<-“ eine Funktion zuweise. Die Funktion spearman_brown() wird also mit der Funktion function() erstellt (kein Witz). Die Funktion function() nimmt die Argumente entgegen, die auch meine neu definierte Funktion spearman_brown() annehmen soll. Die Parameter, die bei der Spearman-Brown-Korrektur eine Rolle spielen, sind der Reliabilitätsschätzer und der Korrekturfaktor. Aus diesem Grund werden die zwei Argumente reliability und factor definiert.

Auf die Definition der Argumente folgt der „Körper“ (engl.: body) der Funktion. Der Körper führt die gewünschte Berechnung durch und verwendet dabei die Funktionsargumente als Variablen. Funktionsargumente sind also nichts anderes als Variablen, die im Innern einer Funktion leben. Der Körper der Funktion wird in geschwungenen Klammern {·} eingeschlossen. Solche Klammern bilden einen abgeschlossenen Block von R-Code; sie werden uns auch im nächsten Kapitel bei der Verwendung von Schleifen wieder begegnen.

In Zeile 5 wird mit der Funktion return() angegeben, dass die Variable corrected_reliability von der Funktion zurückgegeben werden soll. Das heißt: das R-Objekt, das innerhalb der Funktion in die Variable corrected_reliability geschrieben wird, ist der Rückgabewert der Funktion.

6.5.2 Lokale Variablen

Werfen wir noch einmal einen Blick auf den Körper der Funktion spearman_brown(). Wir sehen hier bereits gewohnten R-Code – nichts Besonderes: Variablen werden geschrieben und Berechnungen werden durchgeführt. Ein wichtiger Punkt an diesen Berechnungen ist jedoch, dass sie nur innerhalb der Funktion stattfinden und keine Wirkungen „nach außen“ haben. Was heißt das konkret? Beispielsweise sind alle Variablen, die innerhalb der Funktion definiert werden, sogenannte lokale Variablen. Im Gegensatz zu den lokalen Variablen stehen globale Variablen. Global waren alle Variablen, die wir bislang per <- definiert haben. Solche globalen Variablen werden uns in RStudio im Panel oben rechts unter „Global Environment“ angezeigt.

Lokale Variablen sind außerhalb der Funktion nicht sichtbar und verschwinden nach Aufruf der Funktion wieder.43 Es ist also nicht so, dass die Variablen numerator, denominator und corrected_reliability in die globale R-Umgebung geschrieben werden, wenn ich die Funktion spearman_brown() aufrufe. Das ist extrem nützlich: Ich habe die Variablen numerator und denominator nur definiert, damit mein Code gut lesbar ist und die einzelnen Code-Zeilen nicht zu lang werden.44 Am Ende interessiert mich aber nur der Spearman-Brown-Schätzer als Ergebnis der Berechnung; Variablen, die ich als Zwischenergebnisse abspeichere, interessieren mich hingegen nicht. Wenn ich eine Funktion schreibe, bleiben solche Hilfsvariablen verborgen und nur der Rückgabewert dringt nach außen. Ich kann den Rückgabewert abfangen, indem ich ihn in einer Variablen abspeichere:

Durch diesen Befehl wird eine korrigierte Reliabilität in eine Variable mit dem Namen split_half_correct geschrieben; dass der Rückgabewert der Funktion innerhalb der Funktion in einer Variablen mit dem Namen corrected_reliability abgespeichert ist, ist für das ausgegebene Objekt nicht von Bedeutung.

Argumente sind ebenfalls lokale Variablen in der Funktion. Wenn wir einer Funktion also ein Argument übergeben, definieren wir damit eine lokale Variable mit dem Namen des Arguments innerhalb der Funktion. Daraus können wir beispielsweise schließen, dass im Code der Funktion mean() irgendwo eine Variable mit dem Namen na.rm verwendet wird.

6.5.3 Optionale Argumente

Bei der Definition einer Funktion können wir Standardwerte vergeben und somit optionale Argumente definieren. Wenn wir beispielsweise davon ausgehen, dass wir die Spearman-Brown-Korrektur meistens verwenden, um eine Split-Half-Korrelation zu korrigieren, könnten wir das Argument factor per default auf 2 setzen. Das funktioniert wie folgt:

Diese Schreibweise kennen wir schon vom Aufruf von Funktionen, wenn wir die Argumente mit Namen ansprechen. In diesem Fall können wir die Funktion spearman_brown() auch wie folgt äquivalent verwenden:

6.5.4 Wann schreibe ich meine eigene Funktion

Wie wir in den letzten Abschnitten gesehen haben, ist die technische Definition einer Funktion keine schwierige Sache. Schwieriger ist häufiger die Antwort auf die Frage, wann ich tatsächlich eine Funktion schreiben will. Darauf gibt es keine einzige richtige Antwort, und am Ende muss jeder für sich selbst entscheiden. Generell ist eine sinnvolle Daumenregel, dann eine Funktion zu schreiben, wenn man denselben Code mehrfach geschrieben hat. Häufiges Copy & Paste kann da ein guter Indikator sein. In dem Fall solltet ihr identifizieren, welche Details sich jeweils bei den verschiedenen Varianten des Codes geändert haben, und diese in Argumente umwandeln.

Um zu erkennen, wann Funktionen nützlich sind und welche Variablen man als Argumente umsetzen will, bedarf es sicherlich einiger Erfahrung mit R. Mein Tipp für Anfänger ist deswegen vor allem: Erst mal einfach „coden“ – später Funktionen schreiben. Mit mehr Erfahrung kann sich diese Vorgehensweise ändern. Ich überlege oftmals schon in der Planungsphase eines Projekts, welche Funktionen sich sinnvollerweise anbieten und wie diese zusammen arbeiten sollten. Aber das Vorgehen hängt auch stark von der Art des Projekts ab. Wenn ich bloß Daten einlese und einen t-Test oder eine ANOVA rechne, muss ich dafür keine Funktion schreiben. Wenn ich hingegen viel mit Daten an sich arbeite – also oft Daten auswähle, transformiere und aus bestehenden Werten neue Werte ableite – ergeben eigene Funktionen oftmals mehr Sinn.

6.6 Fragen zum vertiefenden Verständnis

  1. Was ist der Rückgabewert der Funktion str()?
  2. Was ist der Rückgabewert der Funktion hist()?
  3. Kann ich mit der Funktion spearman_brown() gleichzeitig mehrere Reliabilitätsschätzer korrigieren? (Code inspizieren \(\to\) überlegen \(\to\) ausprobieren)

  1. Technisch gesehen sind sogar einfache Berechnungen wie die Addition oder die Auswahl von Elementen per [·] Funktionen. Wir betrachten hier jedoch Funktionen, die dem Schema Funktionsname(Argument1, Argument2, ...) folgen.↩

  2. Interessanterweise können Funktionen sogar anonym sein, also keinen Namen haben. Aber dieser Spezialfall ist für uns erst einmal nicht von Interesse.↩

  3. Das ist natürlich zunächst einmal anders, wenn wir selbst neue Funktionen schreiben. Aber auch dann gilt: Wenn ich die Funktion geschrieben habe und der Berechnung vertraue, kann ich später auf sie zugreifen, ohne mir jedes Mal über die interne Funktionsweise Gedanken zu machen. Das kann eine enorme Arbeitserleichterung sein.↩

  4. Teilweise wurden diese Punkte schon in Kapitel 3 im Abschnitt zur Funktion subset angesprochen.↩

  5. Das ist streng genommen auch wieder eine Vereinfachung. Aber für uns reicht dieses Konzept: Hat ein Argument einen Standardwert, ist es optional; hat ein Argument keinen Standardwert, ist es verpflichtend.↩

  6. Auch wenn es häufig erst einmal der Knackpunkt ist zu wissen, ob es schon eine Funktion gibt, die das eigene Problem löst, wie diese heißt und in welchem Paket ich sie finde.↩

  7. Viele Funktionen können auf verschiedene Arten aufgerufen werden. Das heißt: Sie können mit unterschiedlichen R-Objekten als Eingabe genutzt werden.↩

  8. Wir nehmen interessiert zur Kenntnis, dass c() zwei Argumente mit Standardwerten hat: recursive und use.names. Mit diesen Argumenten haben wir uns bislang nicht beschäftigt und das werden wir auch weiterhin nicht tun. Oftmals „vertraut“ man den Standardwerten, wobei man damit früher oder später auch mal auf die Nase fallen wird.↩

  9. An dieser Stelle ist es sinnvoll, noch einmal zu rekapitulieren, wie hier die Narzissmuswerte der Männer und Frauen ausgewählt werden.↩

  10. Setzt man das Argument var.equal auf TRUE, wird ein klassischer t-Test gerechnet (Standardwert: FALSE). Es ist etwas ironisch, dass die Funktion t.test() keinen klassischen t-Test rechnet. Wenn man das erwartet, könnte man an dieser Stelle auf die Nase fallen, wenn man einfach auf die Standardwerte der Funktion vertraut. Mehr Informationen zum Welch-t-Test finden sich hier: https://en.wikipedia.org/wiki/Welch%27s_t-test.↩

  11. Ein Eintrag einer Liste könnte beispielsweise eine andere Liste sein.↩

  12. Wie bei Variablen ist auch bei Funktionen eine sinnvolle Benennung unerlässlich.↩

  13. Umgekehrt gilt hingegen: Innerhalb einer Funktion kann man auf Variablen der globalen R-Umgebung zugreifen. Ignoriert das jedoch bitte. Werte, mit denen eine Funktion arbeitet, sollten der Funktion per Argument übergeben werden.↩

  14. Es ist guter Stil, die Menge von Code pro Zeile zu begrenzen. Eine Daumenregel ist die Verwendung von nicht mehr als 80 Zeichen Code pro Zeile. Dafür kann es beispielsweise helfen, Zwischenberechnungen in Variablen abzuspeichern. Eigene Funktionen helfen ebenfall dabei, Code lesbar zu gestalten.↩